Tudósok hálózatban

A szegedi matematikai iskola

Matematikusok hálózatban

Matematikus kislexikon

Hatvani László professzor jegyezte le az alábbi történetet: “Pintér Lajossal szigorlatoztattunk Analízisből. Egy hallgatónő rosszul kezdett egy indirekt bizonyítást, mert rosszul tagadta a bizonyítandó állítást. Pintér tanár úr segíteni akart neki, és egy, a mindennapi életből vett példával rá akarta vezetni, hogyan kell az állítást tagadni. Kérte, tagadja a következő állítást: „Minden ember matematikus.” A gyakorlatokon sokszor csinálunk ilyet, és a kolleginának mondania kellett volna a helyes választ: „Van olyan ember, aki nem matematikus.” Felcsillant a szeme, megörült a könnyű kérdésnek, és rávágta: „Nem minden matematikus ember!”
Az alábbi lexikon Intézetünk volt és jelenlegi személyiségeit mutatja be, hosszabb-rövidebb életrajzokkal vagy pár soros portrékkal. Célja, hogy igazolja: minden matematikus ember!
Az életrajzi lexikon egy válogatás jellegű gyűjtemény, az egykor élt kolozsvári-szegedi professzorok és a jelenlegi szegedi matematikusok életrajzait betűrendben tartalmazza. Az életrajzi cikkek nagyon változó mélységűek, tartalmúak és méretűek, az egyes személyiségekről talált, illetve a kortársaktól kapott anyagok függvényében. Az anyaggyűjtés 2021 január-március hónapokban zajlott. A koronavírus-járvány körülményei miatt a személyes kapcsolatfelvétel és az adatgyűjtés az internetre és levelezésre korlátozódott.

 

Kislexikonunk fő és alapvető forrásai voltak a magyar Wikipédia matematikus szócikkei. Az egyes szócikkeknél ezt tételenként külön-külön nem jelöltük, hisz az átvett anyagon módosítottunk, kiegészítettük és rövidítettük stb., projektünk céljainak megfelelően. A felhasználásért ezért itt mondunk együttesen köszönetet!

Aczél János | Benke János Marcell | Brassai Sámuel | Bolyai Farkas és János | Csaba Béla | Csákány Béla | Czédli Gábor | Dénes Attila | Dugonics András | Egerváry Jenő |  Farkas Gyula | Fáry István |  Fejér Lipót | Fodor Ferenc | Fodor Géza | Gécseg Ferenc | Gehér László | Gévay Gábor | Haar Alfréd | Hajnal Péter | Hatvani László | Kalmár László | Kérchy László | Kerékjártó Béla | Kevei Péter | Klug Lipót | Klukovits Lajos | Kosztolányi József | Kozma József | Krámli András | Krisztin Tibor | Kudar János | Kurusa Árpád |  Leindler László | Lipka István | Lovász László | Makay Géza | Maróti Miklós | Martin Lajos| Megyesi László

Következő oldal

Aczél János (1924-2020)

Forrás a képre kattintva látható.

Szülei Aczél Dezső és Adler Irén voltak. 1943–1947 között a Pázmány Péter Tudományegyetem matematika–fizika szakán tanult. Témavezetői Fejér Lipót és Riesz Frigyes voltak. 1945–1948 között az ELTE díjtalan gyakornoka, 1948–1950 között a Szegedi Tudományegyetem tanársegéde, 1950–1952 között a Nehézipari Műszaki Egyetem docense volt. 1952–1959 között a Kossuth Lajos Tudományegyetem tanszékvezető docense, 1959–1965 között tanszékvezető egyetemi tanára volt. Ezután Kanadába ment, ahol a Waterlooi Egyetem matematikaprofesszora lett 1965-ben, 1969-től kiemelt professzora, 1993-tól kiemelt professor emeritus volt. 

1990-ben a Karlsruhei Egyetem, 1995-ben a Grazi Egyetem, 1996-ban a Katowicei Egyetem, 1999-ben a Miskolci Egyetem, 2003-ban a Debreceni Egyetem díszdoktora lett. Öt egyetem (ebből kettő magyar) díszdoktora. A Royal Society of Canada tagja (1971-től), valamint a Magyar Tudományos Akadémia külső tagja volt, 1990 óta.

 a függvényegyenletek és alkalmazásaik az információelméletre, a társadalom- és magatartástudományokra. 

 Császár Ákossal, Fuchs Lászlóval, Gál Istvánnal és Horváth Jánossal együtt a matematika „nagy ötösének” (big five) nevezett, Budapesten működő csoport tagja.

Aczél János Wikipédia URL

Elhunyt Aczél János, a magyar matematika legendás ötösfogatának tagja URL

Tiszteletadás öt kiemelkedő magyar matematikus teljesítményének a Magyar Tudományos Akadémián URL

Benke János Marcell (1989-)

Forrás a képre kattintva látható.

egyetemi adjunktus, Sztochasztika Tanszék

 

Benke János Marcell 1989. április 11-én született Orosházán. Már általános iskolai tanulmányai során

megjelent a matematika iránti érdeklődése. Azonban a tárgy szeretete a makói József Attila Gimnázium nyolcosztályos tagozatán Szilágyi Judit tanárnő matematikaóráin és szakkörein teljesedett ki.

2007-ben kezdte meg tanulmányait a Szegedi Tudományegyetem matematika BSc szakán. Ezen három év alatt nagy hatást tettek rá Németh József, Krisztin Tibor és Röst Gergely órái, melyek felkeltették az érdeklődését a dinamikus rendszerek, azokon belül is az időkésleltetést tartalmazó modellek iránt. Szakdolgozatát Krisztin Tibornál írta Két állapotfüggő késleltetésű differenciálegyenlet numerikus vizsgálata címmel.

2010-ben a Szegedi Tudományegyetem alkalmazott matematikus MSc szakán folytatta matematikai tanulmányait pénzügy-matematika szakirányon. Itt szerette meg a sztochasztikus modellek témakörét Pap Gyula és Szűcs Gábor óráinak köszönhetően. Diplomamunkáját Pap Gyulánál írta Késleltetett

sztochasztikus differenciálegyenletek és alkalmazásuk nem hatékony piacokon címmel. 2012-ben felvételt nyert a Szegedi Tudományegyetem Matematika- és Számítástudományok Doktori Iskolájába, ahol Pap Gyula témavezetésével kezdte meg doktoranduszi tanulmányait.

Ugyanakkor a Lombard Lízing Zrt.-nél kezdett dolgozni kockázatelemző pozícióban, ahol többféle matematikai modell fejlesztésén és implementációján dolgozott.

 

2015 szeptemberétől a Bolyai Intézet tudományos segédmunkatársa, 2019-től adjunktusa, ahol

számos tárgyat oktatott és oktat a valószínűségszámítás, statisztika és sztochasztikus folyamatok témakörében.

 

Szakmai tanulmányai mellett életének fontos területe a zene. Kiskora óta játszik kürtön. Jelenleg két zenekar tagja: a makói Magán Zeneiskola Koncert Fúvószenekarának, illetve a szegedi Universitas Szimfonikus Zenekarnak.

Google Scholar URL

Brassai Sámuel (1797–1897)

Forrás a képre kattintva látható.

Brassói eredetű szász családból, unitárius lelkész fiaként született az erdélyi Torockón (vagy Torockószentgyörgyön), saját bevallása szerint 1797. június 15-én (vagy 1800. február 13.-án) – a halála már biztos: Kolozsvár, 1897. június 24.  Az „utolsó erdélyi polihisztor”, úgy ismert mint aki tíz nyelvet ismert, tíz tudományágat művelt és száz évig élt.

Brassai Sámuel a szülői háznál és a Thoroczkay grófok házában sajátította el a zenét és a természettudományokat, illetve a német nyelvet. (Apja önállóságra nevelte, a tanulás terén is.) Kolozsvárott járt gimnáziumba, majd utazásokat tett Magyarországon és Erdélyben, 21 éves korában pedig nevelőnek állt erdélyi családoknál, ahol zongoratanárként kezdte, később sorban szinte minden fontos tárgy tanításába beletanult. Mi több, olyannyira komolyan vette munkáját, hogy a szaktárgyak megismerésén kívül oktatásmódszertannal is foglalkozni kezdett. 1834-ben hagyta abba a nevelősködést, és Kolozsvárra költözött, ahol megalapította a népművelésre szánt Vasárnapi Újságot, amelyet 1848-ig szerkesztett.  Amikor 1836 augusztusában meghalt a kolozsvári unitárius kollégium rektora, Brassai megpályázta  a helyét. Az Egyházi Képviselő Tanács hosszan vitatta a pályázatot, Brassai ellen több kifogás is fölmerült. Az egyik első, hogy nagy bajusza van (!). A második, hogy nem járt külföldi egyetemeken, hanem helyette főúri házaknál zongorát tanított. Később is sokszor „klavírmester”-nek csúfolták.

A  kolozsvári unitárius főiskolán 1848-ig a történelmet, földrajzot, később matematikát és természettudományokat tanította; 1845-től a bölcselet (mai szóval filozófia) tanára is volt. 1841-től latin helyett magyarul tanított (ez akkoriban nagy szó volt, mert az oktatás hivatalos nyelve az ő fellépéséig a latin volt!). És mivel rájött, hogy a tankönyvirodalom magyar nyelven elhanyagolható, elkezdett sorozatban tankönyveket írni a legkülönfélébb tárgyakhoz.

1848-ban a magyar szabadság híveként katonának állt, 1848 végétől 1849 augusztusáig Bem táborában volt tiszt.

Érdemes belegondolni, hogy ekkor már kb. 50 éves, akkoriban már öregedő embernek számított.

A szabadságharc bukása után Szatmár és Máramaros megyében bujkált, majd 1850-ben Pestre költözött és itt tanárkodott 1859-ig, közben irodalmi kritikákat írt. Ezután visszament Kolozsvárra s az unitáriusok főiskolájában a bölcseletet és matematikát tanította. Ugyanekkor az Erdélyi Múzeum-Egyesület hívta meg a természetrajzi tár őrének és múzeumigazgatónak; ő alapította meg a Mikó-kertben a ma is híres kolozsvári Füvészkertet. Brassai maga mellé vette Hermann Ottót, kit mint az állatgyűjtemény preparátorát alkalmazott.

Amikor a kolzsvári egyetemet létrehozták, nyilvánvaló volt, hogy Brassai valamelyik tanszék élére kerül. Tudományos hírneve, tekintélye miatt (már előtte is több tudományos szervezetben és intézményben fontos szerepet kapott: mint a Természettár őre és a Múzeum-Egylet igazgatója) a lapok sokszor emlegették a jelöltek között. Valójában azt szerette volna, ha a pesti egyetemen a szanszkrit nyelv tanárának hívják meg (1870-ben meg is pályázta), de báró Eötvös József tanügyminiszter megkérdezte, hajlandó volna-e az alapítandó kolozsvári egyetemen valamilyen tanszéket vállalni. A választást Brassaira bízták, aki több tárgyat is megjelölt (filozófia, növénytan, pedagógia, művelődéstörténet, nyelvtudományok és matematika). Az új tanügyminiszternek, Trefort Ágostonnak, amikor végre eljött a döntés ideje, elég nagy fejtörést okozott, „nem könnyen állapodhatván meg abban, melyik tanszékre nevezzék ki”. Végül kinevezték nyilvános rendes tanárnak az Elemi Mennyiségtan tanszékre, amire – Boros György: Dr. Brassai Sámuel élete című könyve szerint – maga Brassai is a legkevésbé számított.

Később a természettudományi kar dékánja, 1879–80-ban pedig egyetemi rektor volt. Még szanszkrit nyelvet és összehasonlító indogermán nyelvészetet is tanított. 1884-ben nyugdíjazták, de ezt követően is fogadott tanítványokat és figyelemmel kísérte a tudományos világ mozgalmait.

Egész életében puritán életmódot folytatott, magára keveset költött, jövedelméből inkább tanítványait támogatta – Herman Ottót pl. a saját fizetésének kb. 1/3-ából fizette. Szeretett gyalogos utazásokat tenni – gyakorlatilag ő volt az egyik első magyar természetjáró – és jól érezte magát egyszerű emberek között. Ragaszkodott a maga által kiszabott napi testmozgás elvégzéséhez: eleinte naponta 5000 lépés, kilencvenéves kora után napi 3000 lépés volt a sétája. Esténként baráti társasága körében zenélt, harmóniumon, brácsán, csellón és zongorán játszott. A szigorú napirendtől csak a zene kedvéért tért el: bármikor kész volt Pestre, Bécsbe vagy akár Berlinbe utazni egy hangverseny kedvéért. Két káros szenvedélye volt, naponta három pipát elszívott, és három deci bort megivott. Mellesleg a szakácsművészethez is konyított: még 90 éves korában is saját készítésű tokánnyal vendégelte meg látogatóit. Soha nem nősült meg, háztartását édesanyja vezette, 90 éves korában bekövetkezett haláláig. (Volt kitől örökölnie a hosszú élet képességét.) Modorát póriasnak tekintették, mert a ráció nevében elutasította a bevett társasági formákat. A korán megőszült, Erdély-szerte „Brassai bácsi”-ként ismert tudósról számos anekdota forgott, amelyek leginkább jóhiszeműségét és szórakozottságát, illetve különcnek aposztrofált szokásait illusztrálják.

Az MTA 1837. szeptember 7-én levelező taggá választotta a matematikai és természettudományi osztályába, majd 1864 januárjában áttették a bölcseleti szakosztályba, illetve 1865. december 10-én rendes taggá választotta a történelmi és filozófiai osztály. Szokatlanul fiatalon, negyvenéves kora előtt választották meg, ezen kívül ő volt a leghosszabb ideig hivatalban levő akadémikus, 1887. május 13-án tiszteleti taggá választották. Az osztályok közötti ide-oda passzolása is egyedi.

Jókai Mór a következőt írta erről:„Látod, tisztelt publikum, ezt a szép hószínű szakállat és hószín hajfürtöket? No, hát tudd meg, hogy ennek minden szála külön tudományban őszült meg. Brassai mindent tud, amit csak tudni lehet: ő nagy filológ, filozóf, matematikus, botanikus, kritikus, historikus, grammatikus, statisztikus, lingvista, belletrista, polémista és jurista; és azonfölül még muzsikus is. Ennek a sokoldalú tudományosságának köszönheti, hogy a Magyar Tudományos Akadémia öt osztálya közül egyikben sem választják meg rendes tagnak. Mert mikor a nagygyűlés napja elkövetkezik, s az osztályoknak ajánlani kellene rendes tagságra kandidátusokat, akkor legelébb is elkezdi a természettudományi és matematikai osztály, hogy mint természettudós is nagy érdemeket szerzett ugyan magának Brassai, de mik ezek azon nagybecsű szolgálatokhoz képest, amiket a magyar irodalomnak a nyelvészet mezején tett; ott volna igazán a helyén; dísze, virága, címere fogna lenni a filológiai osztálynak, s minthogy tíz több, mint kilenc, tehát matematice áll, hogy attól az osztálytól ajánltassék, amelyiknél több az érdeme. A filológiai osztály viszont mély deferenciával elismeri, hogy Brassai a nyelvészetben rendkívüli sikerrel működött, s ha semmi egyebet nem mívelne, mint ezt az egy szőlőjét az Úrnak, bizony be is választaná őt osztályába rendes tagnak; de amidőn Brassai annyira kitűnő filozóf, hogy e hajlama és tanulmánya minden egyéb működésére keresztül-kasul kiterjed, tehát úgy kívánja mind a költői igazságtétel, mind a grammatikai szuperlativusz, hogy ahol „legnagyobb”, oda választassék be: a filozófiai osztályba. A filozófiai osztály végre ezen bölcsészeti dedukciót állítja fel: „ámbátor elismert dolog, hogy Brassai a filozófok között is kitűnő, mindazonáltal már eddig is a természettudományok levelezőtagja levén: tehátlan mind logice, mind naturaliter az következik, hogy ki mely helyen leveledzett, azon helyen virágozzék is; s visszautasítja a kandidációt a természettudósokhoz, s e nemes vetély így foly évről-évre. Brassainak minden osztály égig emlegeti a másik osztályban tett érdemeit s együtt az öt osztály együttes érdemeiért nem választja meg rendes tagnak; hanem végül azt mondja, hogy „mindez semmi! Brassai nagy tudós ugyan, de hát még milyen nagy zeneértő! válassza meg hát a konzervatórium.”  (Jókai Mór: Brassay)

A matematika területén kutatóként nem alkotott maradandót. Kolozsvár matematikai élete abban az időben szegényes volt, matematikai művekhez nemigen juthattak hozzá még a művelt emberek sem, a kor élvonalába tartozó művekhez végképp nem. Tanítványa, Vályi Gyula feljegyzései szerint az „elemi mennyiségtan” tárgykör alá akkoriban az algebra, geometria, trigonometria és „analitica geometria” tartozott, Brassai ezeket adta elő minden tanévben, 1883-ig, nyugdíjazásáig. Ezen kívül ú. n. szakkollégiumokat is tartott: 1876/77-ben Az egyenletek elmélete, 1877/78: Helyzettan – felsőbb geometria, 1880/81: Matézis történelme, 1882/83-ban: Az algebra fejlődése az utóbbi 4 százban. (Mellesleg 1879-1885 között szanszkrit nyelvet és összehasonlító nyelvészetet is tanított, mintegy hobbiból.)

Bár jelentős felfedezés nevéhez nem fűződik, elévülhetetlen érdemeket szerzett a matematika és főleg a geometria oktatásában, tankönyvek és módszertani cikkek írásával. Ő volt az első, aki magyarra fordította és jegyzetekkel látta el Euklidész Elemek című művét (1865-ben).  Több iskolai tankönyvet írt, legjobbnak a „Számító Socrates” címűt tartják.

Számos nyilvános föllépésével az egyik legnagyobb gáncsolója volt viszont Bolyai János elismertetésének. Sajnos, nem ismerte fel Bolyai János új geometriájának korszakalkotó jelentőségét. Emiatt a mai Bolyai Intézet köreiben nem is mondható népszerű személyiségnek…

Számos tudományos értekezést és tudománynépszerűsítő cikket, valamint könyvismertetést és zenekritikát írt, amelyek a következő lapokban, folyóiratokban és egyéb kiadványokban jelentek meg:

Acta Reg. Scient. Claudiop., Akadémiai Értesítő, Athenaeum, Budapesti Szemle, Család és Iskola, Családi Kör, Család Könyve, Divatcsarnok, Egyetemes Philologiai Közlöny, Ellenzék, Emich Gusztáv Nagy Képes Naptára, Erdélyi Hiradó, Erdélyi Múzeum, Erdélyi Múzeum-Egyesület bölcseleti, nyelv és történelemtudományi szakosztály kiadványai, Erdélyi Múzeum-Egyesület évkönyvei, Falusi Gazda, Figyelmező, Figyelő, Flóra, Gazdasági Lapok, Havi Szemle, Hon, Keresztény Magvető, Kolozsvár, Kolozsvári Nagy Naptár, kolozsvári unitárius főiskola értesítője, Korunk, Közoktatási Szemle, Linnaea, Magyar Hírlap, Magyar Nép Könyve és Könyvtára, Magyar Növénytani Lapok, Magyar Nyelvőr, Magyarország és Erdély Képekben, Magyar Polgár, Magyar Pósta, Mezei Gazdaság könyve, Nemzeti Társalkodó, Néptanítók Lapja, Országos Középiskolai Tanáregylet Közlönye, Österreichische Botanische Zeitschrift, Összehasonlító Irodalmi Lapok, Magyar Philosophiai Szemle, Pesti Napló, Szépirodalmi Figyelő, Szépirodalmi Közlöny, Szépirodalmi Lapok, Társalkodó, Természet, Természetbarát, Természettudományi Közlöny, Tudományos Tár, Unitárius Közlöny, Vasárnapi Újság, Zeitschrift für allgemeine Sprachwesen, Zeitschrift für Natur und Heilkunde.

Beszélte a nyugati nyelveket, emellett értett oroszul, szanszkritül, törökül és héberül is. Brassai kívül állt az intézményesedő nyelvészeten, széles nyelvismerete és természettudományos gondolkodása egyedi nyelvészeti gondolkodással ajándékozták meg. A nyelv központi egységének a mondatot, a nyelvészet központi területének a szintaxist tekintette. Különös súlyt fektetett a szórend szerepére, amelyet forradalmian új módon írt le. A topik–fókusz tagolás szabályosságát a látszólag szabad szórendű magyar nyelvben is felfedezte és A magyar mondat (1860–1865) című dolgozatban le is írta azokat a szintaktikai és szupraszegmentális eszközöket, amelyekkel az a magyarban megvalósul. A nyelvtanuló számára is használható generatív modellt dolgozott ki arra, hogyan lehet tetszőleges elemekből érvényes magyar mondatot létrehozni. Bírálta a latin grammatikai hagyományban megrekedt iskolai nyelvoktatást, amely szerinte a diákok többségénél kudarcot vall. Latin, német és francia nyelvkönyvében saját, mondatközpontú nyelvszemléletét érvényesítette. Hangsúlyozta a tanár és a diák közötti élő párbeszéd fontosságát és azt, hogy a szabályokat a diákkal magával, induktív módon kell felismertetni. A reformkorban kidolgozott nyelvpedagógiáját saját maga és a magyar kortársak is az 1880-as években divatossá vált ún. természetes (direkt) módszer előzményének tekintették.Tevékenyen, mindkét oldal álláspontját elutasítva foglalt állást a reformkori nyelvújítás ortológus–neológus vitájában. Saját organikus nyelvszemléletét képviselve elvetette a tudatos, kampányszerű nyelvtervezés szükségét és lehetőségét. Felhívta a figyelmet a paraszti népnyelvre mint a köznyelv lehetséges forrására (!). Tudományos felismeréseit magyarul publikálta, így azokról a (nemzetközi) nyelvtudomány nem is vehetett tudomást. Magyar mondattani eredményei a századforduló után merültek feledésbe. Nyelvkönyvei, kezdeti sikereik ellenére megbuktak a középiskolai grammatikus hagyomány ellenállásán. Közvetlen utókora a különc, autodidakta nyelvészt látta benne. Annak ellenére, hogy a kolozsvári egyetemen a matematika professzora volt, 1879 és 1884 között szanszkrit nyelvet is tanított., 1884/85-ben pedig Összehasonlító nyelvtan és nyelvfilozófia címmel hirdetett előadást. Feljegyezték, hogy sok hallgatója nem azért járt ezekre az órákra, mert a szanszkrit érdekelte volna, hanem az ekkor már legendának tartott öreg tudóst akarták hallgatni. Péntek János nyelvész 2005-ben ezt írta Brassai Sámuelnek a tudományban elfoglalt helyéről: „Még kevésbé igaz az a mostanában (éppen az emlékező rendezvényeken is) hangoztatott, még Kővárytól eredő sommás értékelés, hogy bár több tudományterületen állt kora élvonalában, egyetlen területen sem előzte meg korát. A mondat szerkezetére vonatkozó felismerései, mint az itt közreadott előadásszövegek is bizonyítják, legalább egy évszázaddal megelőzték nem csupán a magyar, de az egyetemes nyelvtudomány korabeli színvonalát.”

„Állított enciklopédizmusom kulcsa az, hogy nekem csak egy tárgyam, egy tudományom van: a módszertan elméletben és gyakorlatban.” (Brassai Sámuel)

Brassai Sámuel tevékenysége fordulópontot jelentett a kolozsvári unitárius főiskola történetében: az ő nevéhez fűződik az 1841-ben végrehajtott tanügyi reform. Ennek fő elemei az alábbiak voltak: a latin tanítási nyelv eltörlése; a tanítók kinevezése ne osztályonként, hanem hét szak szerint történjen: latin, magyar–német, olvasás- és értelemkifejtő gyakorlatok, természetrajz, földrajz–történelem, szám- és űrtan, írás, rajzolás, ének és vallás; állandó nevelésügyi bizottság létesítése, pedagogarkai állás létesítése (a pedagogarka feladata az volt, hogy a végzős diákok közül kiválassza a legjobbakat, akiket azután felkészített a tanítás módszereire). A zsinat minden vita nélkül elfogadta a tervet és elrendelte azonnali életbeléptetését. Brassai az oktatás tárgyi feltételeinek megteremtésére megindította a Kék könyvtár tankönyvsorozatot, amelybe maga is számos kötetet írt: A számító Socrates, A kisdedek számvetése, Rajzminták fiatal gyermekek számára, Okszerű vezér a német nyelv tanításában, Fiatal kereskedők arany ábécéje, Algebrai gyakorlókönyv. Adományokkal járult hozzá a vegytani és fizikai szemléltetőeszközök beszerzéséhez, a könyvtár gyarapításához, ezen kívül a zenei oktatás céljára harmóniumot is ajándékozott. A népiskolai törvény (1868) hatályba lépését követően módszertani könyvet és példatárat állított össze a néptanítók számára. Az oktatást illetően Brassai fő elve az volt, hogy keveset, lassan és jól kell tanítani:

„az igazi műveltséget is bizony nem az ismeretek sokasága, hanem korlátolt számú, jól rendezett, ép, egészséges eszmék s a megszerzésükben és által gyakorlott, élesített és szaporító érlelő tehetség jellemzi.”

A tanítás során figyelembe kell venni a tanítvány képességi szintjét, és fel kell kelteni érdeklődését. Fontosnak tartotta a szemléltetést és az ismétlést. Figyelemmel kísérte az olvasó- és vitaegyletek munkáját, bátorította a diákok irodalmi próbálkozásait. A korban szokásos tekintélyelvű, szónokias oktatás helyett kérdésekkel vezette rá tanítványait az ismeretekre, az ifjakat barátaiként kezelte.

1836-ban jelent meg „A füvészet elveinek vázlata” c. munkája, több növényrendszertani művet írt. Megalapította a kolozsvári Füvészkertet, aki köré szerveződött a későbbi Tudományegyetem növény-és állattani képzése. Leghíresebb tanítványa Herman Ottó volt. A nemzetközi botanikában akkora tekintélyre tett szert, hogy Endlicher, a bécsi természettudományi múzeum botanikusa róla nevezett el egy ausztráliai növényt, a Brassaia aetinofilla-t. Közgazdaságtan
1842-ben jelent meg Bankismeret c. műve – meglepően alapos áttekintés, célja, hogy a reformkori Erdély viszonyai között a pénzügyi-gazdasági ismereteket terjessze, mivel ezt is az általános műveltség szükséges részének tartotta. Gazdasági nézeteivel Széchenyit támogatta.

Ő írja az egyetlen komoly bírálatot Eötvös József A XIX. század uralkodó eszméi c. művéről (Magyar Hírlap. 1851, 522-528. p.)

Talán legkedvesebb időtöltése a zene volt. Személyes barátja volt Erkelnek, aki ifjúkorában Kolozsvárott volt zenetanár. Liszttel azonban vitatkozott a magyar zene kérdésében: „Magyar- vagy cigányzene” című röpiratában világos különbséget tesz a kettő között. 1856-tól a Magyar Hírlap zenekritikusaként is dolgozott. Nagy zeneszerzőkről írott találó portréi ma is élvezhetőek lennének.

Ezzel a kérdéskörrel 50-es éveiben kezdett foglalkozni. Logika című művében, 1858-ban a megértés kérdéseivel foglalkozott, és a filozófiát lélektani alapon képzelte el. Vitatkozott a hegeliánusokkal, de a materialistákkal is (később, a marxista utókor nem is kedvelte őt emiatt). De saját kortársaival is kemény vitái voltak: „Az exact tudományok követelései a philosophia tárgyában” c. értekezését a Tudományos Akadémia nem fogadta el, majd amikor Brassai 1862-ben megjelentette „Az Akadémia igazsága” című vitairatát, melyben megvédi álláspontját, az Akadémia III. osztályából ekkor teszik át a II.-ba. Voltak vitái az atomelmélet és a pozitivizmus híveivel is. Még 95 évesen is írt dolgozatot „Igazi pozitív philosophia” címmel.

  • Bévezetés a világ, föld és státusok esmeretére. Kolozsvár, 1834
  • A füvészet elveinek vázolata. Lindley János nyomán. Kolozsvár, 1836
  • Számító Sokrates. Fejbeli számolás kérdésekben. Angol mintára hazai viszonyokhoz alkalmazva. Kolozsvár, 1842
  • Bankismeret. Kolozsvár, 1842 (Ism. Athenaeum)
  • A kisdedek számvetése angol mintára. Kolozsvár, 1842
  • Rajzminták fiatal gyermekek számára. Angol előkép után magyarázó szöveggel. Kolozsvár, 1842
  • A fiatal kereskedő arany abc-je. Montag R. J. után. Kolozsvár, 1847. (Kereskedői Könyvtár I. köt.)
  • Okszerű vezér a német nyelv tanulásában. Kolozsvár, 1845. Két rész
  • Algebrai gyakorlatkönyv és kulcsa. Pest, 1853–57. Két rész
  • Logika lélektani alapon fejtegetve. Pest, 1858
  • Tigrisvadászat Indiában. Rice William után ford. Pest, 1859
  • Az árnyékóra. (Ugyanott, 1859 (M. Akadémiai Értesítő XIX. 4.)
  • A magyar mondat. Pest, 1860–63. Három közlés
  • Magyar vagy czigány zene. Elmefuttatás Liszt Ferencz: Czigányokról irt könyvére. Kolozsvár, 1860
  • Irodalmi pör a filozofia ügyében (species facti), melyben a tanuságot és botrányt kedvelő több mulatságot fog találni, mint népszerűtlen czíméből itélve gyanítaná. Kolozsvár, 1861
  • Az akadémia igazsága. Kolozsvár, 1862
  • Ingyen tanító franczia nyelvmester. Kolozsvár, 1863. I. rész
  • Nem csak az anyag halhatatlan. Kolozsvár, 1865
  • Euklides elemei XV könyv. Pest, 1865
  • A módszerről. Pest, 1867–69. Három értekezés. Székfoglaló a tört. philos. osztályban
  • A magyar bővített mondat. Pest, 1870
  • Számtan a népiskolákban. Az I. és II. osztály tanítója számára. Vezérkönyv és példatár. Pest, 1872. Két rész
  • Számvetés a népiskolában a II. oszt. tanítványok számára. Pest, 1872
  • Hogy kelljen a latin hajtogatást észszerűen gyorsan és sikeresen tanítani? Pest, 1872
  • Commentator commentatus. Tarlózások Horatius satiráinak magyarázói után. Pest, 1872
  • Paraleipomena kai diorthoumena. A mit nem mondtak s a mit roszul mondtak a commentatorok Virg. Aeneise II. könyvére. Különös tekintettel a magyarokra. Budapest, 1873
  • Laelius. Hogyan kell és hogyan nem kell magyarázni az iskolában a latin autorokat? Kolozsvár, 1874.
  • A neo- és palaeologia ügyében. Budapest, 1875
  • A gyógyszerészné. Beszély gróf Sollogub után oroszból ford. Budapest, 1877
  • Logikai tanulmányok. Budapest, 1877
  • A nyelvujítás és Ballagi. Kolozsvár, 1881
  • A magyar nyelv ellenőre. Kolozsvár, 1881–82 (I. és II. fogás)
  • A mondat dualismusa. Budapest, 1884
  • Algebrai gyakorlatok. Budapest, 1883–84. Két rész
  • Nézetek a vallás eszméjéről. Kolozsvár, 1887. Három értekezés
  • Szórend és accentus. Budapest, 1888
  • Vallás és hit. Kolozsvár, 1887
  • A Jézus istensége. Kolozsvár, 1887
  • A növény nevek leirása. Kolozsvár, 1888
  • Az igazi positiv philosophia. Budapest, 1895

Magyar életrajzi lexikon I. (A–K). Főszerk. Kenyeres Ágnes. Budapest: Akadémiai. 1967. 262. o.
Szinnyei József: Magyar írók élete és munkái I. (Aachs–Bzenszki). Budapest: Hornyánszky. 1891.
Concha Győző: Brassai Sámuel emlékezete. Budapest: Franklin-Társulat. 1904.
Fitz József: Brassai Sámuel monografia. Budapest : Németh József, 1911.
Brassai százéves pályafutása URL 
Wikipédia URL
Oláh-Gál Róbert, Sándor József:   Brassai Sámuel, a kolozsvári egyetem első matematikaprofesszora  (Műszaki Szemle, 54. sz. 2011.) URL 

Bolyai Farkas (1775-1856)

Forrás a képre kattintva látható.

Bolyai János (1802-1860)

Forrás a képre kattintva látható.

Nem voltak egyetemünk professzorai, viszont a magyar matematika korai történetének vezéralakjai, az Intézet róluk van elnevezve.

Bolyai Farkas Wikipédia URL

Agora: Bolyai Farkas URL

Bolyai Farkas életének és munkásságának eseményei URL

Bolyai János Wikipédia URL

Bolyai János Forradalma URL

Bolyai János életútja URL

Csaba Béla (1968-)

Forrás a képre kattintva látható.

egyetemi docens

Halmazelmélet és Matematikai Logika Tanszék

A következőket írta magáról:

1968-ban születtem Békéscsabán. Általános iskolám a csabai 1-es iskola volt, ott a felsőben Michelsz Lászlóné volt a matektanárom. Utána a Rózsa Ferenc gimnáziumba jártam (mára szerencsére nevet változtatott, Andrássy Gyula a neve). Harmadiktól Bajnok Zoltán tanította nekem a matematikát. Mára mindketten nyugdíjasok, nagyon remélem, egészségesek.

2000-ben nyertem PhD fokozatot, 2016-ban pedig habilitáltam matematika- és számítástudományok témából a Szegedi Tudományegyetemen.

 Mi indított el a pályán? Jó matektanárom volt gimnáziumban, de akkor még jobban érdekelt a fizika. Aztán Szegeden, az egyetemen valahogy fokozatosan belekeveredtem a matematikába. Hajnal Péternek, akkor tanáromnak, ma már kollégámnak különösen sokat köszönhetek.

Valószínűleg három matematikustól tanultam a legtöbbet, ők Szemerédi Endre, Beck József és Komlós János. A Rutgers egyetemen voltam doktorandusz, ahány doktori kurzust csak tartottak, mind felvettem, emellett sokat beszélgettünk. A témavezetőm Szemerédi Endre volt, igazi óriása a kombinatorikának és a számelméletnek.

Mai matematikai érdeklődésemet, munkámat is meghatározza, amit hármójuktól tanultam.

Ha ráérek, a sport a fő kedvtelésem, nézni és csinálni is szeretem. Sportok, amiket űzök (mostanában sokszor inkább csak űznék): úszás, kajak, futás, kondipark. Amiket nézek: tulajdonképpen az USA profi sportjaitól és a motorsportoktól eltekintve szinte minden érdekel. Azért leginkább a futball.

  • Online algoritmusok: főként a k-server és online párosítási problémák, véletlen modellek, megszorított feladatok
  • Gráfelmélet: regularitási lemma, extremális kérdések (Bollobás-Eldridge, Ore-fok, fák lerakása, más típusú pakolások), expanderek, véletlen gráfok, speciális gráfosztályok 
  • Algoritmusok: kombinatorikus optimalizálási feladatok várható költsége, metrikus terek közelítései, véletlen algoritmusok

Egy kis történet jut most eszembe, amit még Beck József egy óráján hallottam. Számelméletről beszélt, Vinogradov egy híres eredményét vezette be. Elmondta, hogy Vinogradov, bármily kiváló matematikus volt is, embernek nem volt épp a legjobb. Ennek talán az volt az oka, hogy már kisgyerekként felismerte matematikai tehetségét, onnantól már csak a matematikára összpontosított. Merthogy sokan úgy vélik, ha valaki észreveszi, hogy tehetséges a matematikában, más már nem tudja igazán lekötni, jellemfejlődése megreked. Ekkor valaki a hallgatók közül megkérdezte: És ön hány éves volt, amikor felismerte, hogy tehetséges matematikus? Beck válasza: Harminchét.

Letölthető cikkei URL

Csákány Béla (1932-2022)

Csákány Béla (1932-)

Forrás a képre kattintva látható.

Csákány Béla (Karcag, 1932. szeptember 18.) matematikus, egyetemi tanár.

Kutatási területe: absztrakt algebra, ezen belül elsősorban univerzális algebra, ezen belül főleg a varietások és a klónok elmélete. Diszkrét matematikai játékok.

Felsőfokú tanulmányokat a szegedi egyetem matematika-fizika szakán folytatott 1951–1955 közt, 1955-ben nyert matematika-fizika szakos középiskolai tanári oklevelet. Végzés után bekerült a Bolyai Intézet Rédei László által vezetett Algebra és Számelmélet Tanszékére. 1958–1961 között Moszkvában, a Lomonoszov Egyetemen volt aspirantúrán. 1962-ben érte el a kandidátusi tudományos fokozatot. 1964. augusztus 1-jén egyetemi docensnek nevezték ki. 1968-tól 1993-ig vezette az Algebra és Számelmélet Tanszéket. 1969-től 1972-ig ő volt a József Attila Tudományegyetem tudományos rektorhelyettese, majd 1985 és 1990 között rektora.

A matematika tudományok doktora fokozatot (DSc) 1975-ben érte el a Malcev-típusú tulajdonságok és alkalmazásaik témakörben. Egyetemi tanárnak 1976. július 1-jén nevezték ki. 1982-ben 4 hónapot Kanadában (Université de Montréal) töltött mint vendégkutató. 1991-ben 5 hónapig vendégprofesszor volt Amerikában (University of Louisiana at Lafayette, Louisiana Állam). 2005-ben az MTA elnöksége már mint a Bolyai Intézet professor emeritusát Eötvös József-koszorúval tüntette ki. Nemcsak kiváló kutató, hanem kiváló tanár is, hivatalosan 12  tanítványa van.

Matematikai tudományos közleményeit nemzetközi nyelveken, oroszul, németül és angolul adta közre, 1970-től csak angolul, ahogyan ez a természettudományokban szokás.

Absztrakt algebra, ezen belül elsősorban univerzális algebra, ezen belül főleg a varietások és a klónok elmélete. Diszkrét matematikai játékok.

  • Diszkrét matematikai játékok (1998) (Ser. Szeged, Polygon. (Ser. Polygon könyvtár , 1218-4071 ; 7.)
  • Kis matematikai szintézis (2003). Szeged, Polygon.
  • The solitaire army reinspected, with Juhász, Rozália. (Mathematics Magazine, Vol. 73, No. 5, pp. 354–362.)
  • Primitive Klassen von Algebren, die zu Klassen von Halbmoduln und Moduln \aquivalent sind. (Acta Sci. Math. 24, 157-164 (1963).)
  • Uber Abelsche Eigenschaften primitiver Klassen universeller Algebren. (Acta Sci. Math. 25, 202-208 (1964).)
  • Inner automorphisms of universal algebras. (Publ. Math. 12, 331-333 (1965).)
  • Uber den Graphen der Untergruppen einer endlichen Gruppe, with Pollák, G. (Czech. Math. J. 19(94), 241-247 (1969).)
  • Translations of regular algebras, with Schmidt, E. T. (Acta Sci. Math. 31, 157-160 (1970).)
  • Characterizations of regular varieties. (Acta Sci. Math. 31, 187-189 (1970).)
  • Congruences and subalgebras. (Ann. Univ. Sci. Budapest. Rolando Eoetvoes, Sect. Math. 18(1975), 37-44 (1976).)
  • Varieties of modules and affine modules. (Acta Math. Acad. Sci. Hung. 26, 263-266 (1975).)
  • Varieties in which congruences and subalgebras are amicable. (Acta Sci. Math. 37, 25-31 (1975).)
  • On affine spaces over primefields. (Acta Sci. Math. 37, 33-36 (1975).)
  • Varieties of idempotent medial quasigroups, with Megyesi, László. (Acta Sci. Math. 37, 17-23 (1975).)
  • Varieties of affine modules. (Acta Sci. Math. 37, 3-10 (1975).)
  • Conditions involving universally quantified function variables. (Acta Sci. Math. 38, 7-11 (1976).)
  • Varieties whose algebras have no idempotent elements. (Colloq. Math. 35, 201-203 (1976).)
  • Contributions to universal algebra. Colloquium on universal algebra at the József Attila University in Szeged from August 26 to August 29, 1975. Host: The Bolyai János Mathematical Society, with Schmist, J. (ed.). (Colloquia Mathematica Societatis Janos Bolyai. 17. Amsterdam -Oxford – New York: North-Holland Publ. Co. 607 p. \$ 81.75; Dfl. 200.00 (1977).)
  • Homogeneous algebras. (Contributions to general algebra, Proc. Klagenfurt 1978, 77-81 (1979).)
  • Inductive clones., with Gavalcova, T. (Finite algebra and multiple-valued logic. Szeged 1979, Colloq. Math. Soc. Janos Bolyai 28, 115-126 (1981).)
  • Varieties of idempotent medial n-quasigroups, with Megyesi, László. (Colloq. Math. 42, 45-52 (1979).)
  • Finite homogeneous algebras. I., with Gavalcova, Tatjana. (Acta Sci. Math. 42, 57-65 (1980).)
  • Homogeneous algebras are functionally complete., (Algebra Univers. 11, 149-158 (1980).)
  • Homogeneity and completeness.(Fundamentals of computation theory, Proc. int. FCT-Conf. Szeged/Hung. 1981, Lect. Notes Comput. Sci. 117, 81-89 (1981).)
  • Three-element quasi-primal algebras, with Cavalcova, Tatjana. (Stud. Sci. Math. Hung. 16, 237-248 (1981).)
  • Finite algebra and multiple-valued logic, with Rosenberg, I.(ed.). (Colloquium held in Szeged, August 27-31, 1979)., (Colloquia Mathematica Societatis Janos Bolyai, 28. Amszterdam – Oxford – New York: North-Holland Publishing Company. 880 p. \$ 135.00; Dfl. 290.00 (1981).)
  • Universal algebra, with Fried, E. (ed.); Schmidt, E. T. (ed.). (Proceedings of the Colloquium on Universal Algebra held in Esztergom, Hungary, from June 27 to July 1, 1977)., (Colloquia Mathematica Societatis Janos Bolyai, 29. Amsterdam -Oxford – New York: North-Holland Publishing Company. 804 p. \$ 151.00; Dfl. 325.00 (1982).)
  • All minimal clones on the three-element set. (Acta Cybern. 6, 227-238 (1983).)
  • Three-element groupoids with minimal clones. (Acta Sci. Math. 45, 111-117 (1983).)
  • On conservative minimal operations., (Universal algebra, Colloq. Szeged/Hung. 1983, Colloq. Math. Soc. János Bolyai 43, 49-60 (1986).)
  • Selective algebras and compatible varieties. (Stud. Sci. Math. Hung. 19, 431-436 (1984).)
  • Completeness in coalgebras., (Acta Sci. Math. 48, 75-84 (1985).)
  • Iskander, A.A.: Solvability of equations in varieties of universal algebras., (Acta Math. Univ. Comen., New Ser. 62, No.2, 169-178 (1993))
  • Life is functionally complete. (Algebra Univers. 30, No.1, 149-150 (1993).)
  • Varieties generated by finite homogeneous algebras, with Szederkényi, A. (Algebra Univers. 30, No.3, 337-344 (1993).)
  • Proving Magari’s theorem via a Mal’cev-type result., with Chajda, I. (ed.) et al. General algebra and ordered sets. Proceedings of the international conference and summer school, held in Horn\'{\i} Lipov\’a, Czech Republic, September 4-12, 1994. Olomouc: Palack\’y University Olomouc, Department of Algebra and Geometry, 31-32 (1994).)
  • Magari via Malcev., (Algebra Univers. 36, No.3, 421-422 (1996). [ISSN 0002-5240; ISSN 1420-8911)
  • Algebras whose subalgebras and reducts are trivial, with Kearnes, K. A. (Acta Sci. Math. 63, No.3-4, 379-381 (1997).)
  • Associative spectra of binary operations, with Waldhauser, Tamás (Multiple Valued Logic, 2000, Voll. 5, pp. 175–200.)
  • A form of the Zermelo-von Neumann theorem under minimal assumptions. (Acta Cybernetica 15(2002) 321-325)
  • Matematika. [Matematika Intézet, 1929-től Bolyai Intézet története]. Varga Antallal. In A Szegedi Tudományegyetem múltja és jelene: 1921-1998 = Past and present of Szeged University. /JATE. Szeged : Officina Ny., 1999. 380-402. p.
  • A második triumvirátus: Triptichon alulnézetből. Szeged : a város folyóirata. 12 (11) 2000, 21-33. p.
  • Rédei László utolsó dolgozatáról. Polygon, 10 (2) 2000, 17-22. p.
  • A két Bolyai : szobrok az intézet előcsarnokában. Szeged : a város folyóirata, 14. 2002:12, 37. p.
  • Egy szegedi néptanító emlékezete : portrévázlat Gáspár Dezsőről. Bakacsi Gézával. Szeged : a város folyóirata, 15.2003:2, 22-27. p.
  • Kalmár László : (1905-1976). Szegedi műhely, 44.2005:2, 115-121. p.
  • Kalmár László: Kalmárium : Kalmár László levelezése magyar matematikusokkal : [I-II. köt.] / összeáll., [előszó:] Szabó Péter Gábor ; [lektorálta: Csákány Béla] Szeged : Polygon, 2005-2008. (Polygon Könyvtár ; 15., 17.)
  • 90 éves a szegedi természettudományos képzés (A matematikáról szóló fejezetet írta) 173-198. p.  URL
  • Anekdoták a Bolyai Intézetből URL
  • Miért lettem matematikus? Szerk. Róka Sándor. Budapest, Typotex, 2003. p. 48-58 URL
  • Csákány Béla: Móra, méhek, matematika. (in: Ponticulus Hungaricus, évfolyam 7–8. szám · 2010. július–augusztus) URL
  • Csákány Béla: Móra matematikusai  (in: Ponticulus Hungaricus, évfolyam 7–8. szám · 2010. július–augusztus) URL
  • https://www.citatum.hu/szerzo/Csakany_Bela URL
  • Tudományos Minősítő Bizottság, Matematikai Szakbizottság, tag (1967—1973)
  • MTA Matematikai Szakbizottság, tag (1985—)
  • SZTE Matematika- és Számítástudományok Doktori Iskola (témavezető)
  • Bolyai János Matematikai Társaság (1962—)
  • Magyar partizán emlékérem (1957)
  • Munka érdemrend ezüst fokozat (1969)
  • Szele Tibor-emlékérem (1981)
  • Munka érdemrend arany fokozat (1982)
  • Akadémiai Díj (1994)
  • Szent-Györgyi Albert-díj (1996)
  • Szegedért Alapítvány Szőkefalvi-Nagy Béla-díja (2002)
  • Eötvös József-koszorú (2005)
  • Aranydiploma (2005)
  • Gyémántdiploma (2015)
  • a matematika története
  • hegymászás, egészen komoly méretekben! 1996-ban fiával együtt megmászta a Kilimadzsárót URL
  • bumeráng gyűjtés

Lenyűgöző anekdota-gyűjteményeket állított össze kollégáiról. Szerénysége megakadályozta abban, hogy önmagáról is feljegyezzen párat. Egy-kettőt összeszedtünk:

 

  1. Miért aprítják a hallgatókat algebra vizsgán? Mert dolgozik a CSÁKÁNY! (Csákány Béla professzor úr tanította az algebrát.)

 

Forrása:

Szent-Györgyi lovon? Válogatás a Szegedi Tudományegyetem Természettudományi és Informatikai Karának anekdotakincséből / szerk. Szabó Péter Gábor.. Szeged, Szegedi Tudományegyetem TTIK, 2014.

 

Egy másikat Szilassi Lajos tanár úr mesélt:

 

Az 1961-62-es tanévben az akkori első évfolyamnak Szendrei János professzor úr tartotta

az algebra előadást.

(Évfolyamtársaim: Hatvani László, Hegedűs Jenő, Dömösi Pál, Visy Gábor megerősíthetik a

történetemet, Makay Árpád, Krámli András sajnos már nem. Itt jegyzem meg a fiatal

generáció számára: a felsoroltak közül hárman később a matematikai tudományok doktora

-ú.n. nagydoktor – lettek.)

 

 Olyan kristálytiszta, szépen felépített előadásokat hallhattunk, hogy a vizsgaidőszakban

nem azért tanultuk teljes erőbevetéssel az anyagot, hogy jó jegyet kapjunk, hanem azért,

mert ott süllyedtünk volna el szégyenünkben, ha nem tudtuk volna a tőlünk telhető módon

legjobban visszaadni azokat a csodálatosan felépített szép fogalmakat, tételeket,

bizonyításokat amiket a két félév során hallottunk.

 

  1. szeptemberében futótűzként terjedt el a hír, hogy Szendrei professzor úr átment a

tanárképző főiskolára. Szorongva vártuk az első algebra órát a Bolyai teremben. (Másutt

nem fértünk volna el.)

 

Bejött egy gyerekképű, vékony, szőke, fiú, fekete keretes szemüvegben, kiállt a dobogó

szélére, és ez volt az első mondata: Csákány Béla vagyok, én fogom tanítani az algebrát,

tegezzetek.

 

Összenéztünk, és talán mindannyian arra gondoltunk, ezt a fiút megesszük reggelire. Hol

lesz Ő az elődjéhez képest?

Az első óra végére kiderült, hogy az Ő előadása épp olyan világos, érthető, szépen

felépített , jól jegyzetelhető* mint amilyet az előző évben megszoktunk. Pillanatok alatt

kialakította azt az emberi és szakmai tekintélyt, ami arra késztetett bennünket, hogy

továbbra is ugyanolyan lelkesen tanuljuk az algebrát.

 

* Azokban az években természetes körülménynek tekintettük, hogy minden tárgy első

előadása így kezdődött: “Ehhez a tárgyhoz írott jegyzet vagy tankönyv nincs, azt   – és

csak azt – kell tudni a vizsgán, ami itt elhangzik.”

  • Szegedi egyetemi almanach : 1921-1995. I. köt. (1996). Szeged, Mészáros Rezső. Csákány Béla lásd 260-261. p. ISBN 963-482-037-9
  • Szegedi egyetemi almanach : 1921-1970. Szeged, Márta Ferenc – Tóth Károly, 1971. Csákány Béla lásd 136. p.
  • Csákány Béla matematikus Wikipédia oldala URL
  • http://www.math.u-szeged.hu/~csakany/csbela.jpg
  • http://www.math.u-szeged.hu/~csakany/

  • Magyar Örökség a Szegedi Tudományegyetem Bolyai Intézete – Dr. Csákány Béla … 13. URL

Czédli Gábor (1953-)

Czédli Gábor

Forrás a képre kattintva látható.

Budapesten született, 1953-ban. Baján a III. Béla Gimnáziumba járt, itt kezdett el érdeklődni a matematika iránt. 1971-ben érettségizett. Középiskolai matematikai versenyek, a Középiskolai Matematikai Lapok (KÖMAL), és Hegedűs József tanár úr hatására jelentkezett és nyert felvételt a József Attila Tudományegyetemre (JATE). Tizenegy hónapos sorkatonai szolgálat és öt egyetemi esztendő után 1977-ben kitüntetéses matematikusi oklevelet kapott a JATE-n. Diplomázást követően (egy fél éves 1982-es kanadai tanulmányutat leszámítva) folyamatosan Szegeden, a Szegedi (2000 előtt: József Attila) Tudományegyetem Bolyai Intézetében dolgozott 2020. szeptemberi nyugdíjba vonulásáig; 1997-2020 között a professzorként. 1999-2005 között a Bolyai Intézet, 2004-2007 között az Algebra és Számelmélet Tanszék, 2008-2020 között pedig a Matematika és Számítástudományok Doktori Iskola vezetője volt.  A kandidátusi fokozatot 1984-ben, a Matematikai Tudomány Doktora címet 1996-ban szerezte meg.  Még egyetemi hallgató volt, amikor mestere, Huhn András (és részben Csákány Béla) irányításával a tudományos kutatást elkezdte; a kandidátusi fokozat megszerzése során pedig Schmidt Tamás tanítványa volt.

Kutatási eredményeit e sorok írásakor 166 tudományos cikke és egy monográfiába írt fejezet tartalmazza. A 166 cikkből 160 már megjelent nemzetközi matematikai folyóiratokban. Ezek témája az algebrán belül főleg a hálóelmélet (nem tévesztendő össze a hálózatok elméletével) és másodsorban az univerzális algebra, de van egy-két más területhez (pl. a geometriához) tartozó tudományos cikke is.

Három tanítványa is tudományos fokozatot szerzett: Takách Géza 1999-ben, Katonáné Horváth Eszter 2005-ben, Skublics Benedek 2013-ban védte meg PhD dolgozatát. 

Az Algebra és Számelmélet Tanszék profiljához tartozó legtöbb tárgyat oktatta és öt tankönyve jelent meg. Emellett előfordult, hogy pályája elején bevezető analízist (mai nevén kalkulust) vagy mellékállásban programozást tanított. 

Hazánkban ő volt az első oktató, aki ˝Zsonglőrködés és matematika” témából (és ezen a címen) egyetemi kurzust hirdetett; 2005-2007 között három alkalommal, nem csak matematikus hallgatóknak. A matematikai elmélet segítségével megtervezett zsonglőrminták közül sokat be is mutatott. A félév végén csak az mehetett vizsgázni, aki három labdával 10 elkapásig eljutott – ez a próbatétel azonban nem csökkentette ennek a szabadon választható kurzusnak a népszerűségét.

Hobbija egy időben a sakkozás volt. A Bolyai Intézetben több mint egy évtizeden át úgy kb. 2005-ig évente megrendezett oktatók és hallgatók közötti háromtusa mérkőzések (foci, pingpong, sakk) alkalmából az oktatói sakkcsapat tagja volt. Ezt követően majd egy évtizedig lelkes amatőr zsonglőr. Napjainkban amatőr szinten zenélni tanul, de fő hobbija változatlanul a matematika kutatása.

  • 1976: Rényi Kató Emlékdíj II. fokozata (Bolyai J. Mat. Társulat)
  • 1977: Schweitzer Miklós Matematikai Emlékverseny III. helyezés (Bolyai J. Mat. Társulat)
  • 1981: Grünwald Géza Emlékdíj (Bolyai J. Mat. Társulat)
  • 1987: “Kiváló Munkáért” kitüntető jelvény (Minisztertanács)
  • 1994: Akadémiai Díj (MTA, négy díjazott között megosztva)
  • 1997: Széchenyi Professzori Ösztöndíj (Művelődési és Közoktatási Minisztérium, 4 évre)
  • 2003: Magyar Köztársasági Arany Érdemkereszt (a Köztársasági Elnöktől)
  • 2016: Magyar Érdemrend Tisztikeresztje (a Köztársasági Elnöktől)
  • 2016: Szőkefalvi-Nagy Béla Érem
  • 2016: Birkhäuser-Grätzer Prize 
  • 2017: Pro Universitate díj
  • 2021: Professor Emeritus cím
  • Czédli Gábor: Hálóelmélet URL
  • Bálintné Szendrei Mária – Czédli Gábor – Szendrei Ágnes: Absztrakt algebrai feladatok URL
  • Czédli Gábor: Szerkeszthetőségi feladatok URL

 

Ez utóbbi címlap kapcsán e sorok írója beismeri, hogy elsősorban az állatképek miatt tetszett meg (végre valami, amit egy laikus is megért…) Czédli professzor azonban az állatképekre olyan magyarázatot adott, ami számomra teljes újdonságot jelentett. 

Tehát:

“A vastag vonallal jelölt négy adatból a húrnégyszög megszerkeszthető (és azért a cica szerepel ábraként, mert az barátságos állat), de a három vastag vonallal jelölt adatból a háromszög (a szokott eljárással)  éppúgy nem szerkeszthető meg, ahogy a “kör nem négyszögesíthető” (a rinocérosz barátságtalan állat).”

(Czédli professzor úr szíves megjegyzését lejegyezte: Tandori Mária)

Dénes Attila (1982-)

Forrás a képre kattintva látható.

Békéscsabán született, 1982-ben. A Rózsa Ferenc Gimnáziumba járt 1996-2000 között. A SZTE matematikus szakát 2005-ben végezte el. 2011 ben nyerte el a PhD fokozatot.

Doktori disszertációja címe: Populációdinamikai rendszerek elméleti és számítógépes stabilitásvizsgálata. Témavezetője Hatvani László professzor.

Bár sok minden érdekelt általános és középiskolás koromban, igazából elég korán egyértelművé vált, hogy matematikával szeretnék foglalkozni, mindig ezt találtam a legszebbnek, ezt élveztem a legjobban. Az első versenyekre általános iskolás koromban édesapám készített fel. Gimnazistaként a legnagyobb hatással Nagy Sándor tanár úr volt rám, akivel a versenyekre készültem és akinek feladatmegoldó képessége és kedvessége is lenyűgözött.

Amikor matematikusnak jelentkeztem az egyetemre, még nem volt pontos elképzelésem arról, hogy mit is fogok csinálni, azonban aligha gondoltam, hogy egyszer járványok terjedését fogom modellezni. Egyetemi éveim alatt Hatvani László professzor úr előadásai és személyisége ragadott meg a legjobban, később Hatvani professzor úr lett a doktori témavezetőm is.

Doktori fokozatszerzésemet követően Röst Gergelynek köszönhetően kapcsolódtam be a matematikai epidemológiai kutatásokba.

Legkedvesebb hobbijaim az olvasás, a nyelvtanulás, angolul, németül, olaszul, franciául, spanyolul és portugálul beszélek. Szeretek utazni, matematikusként is számos lehetőségem nyílt távoli országokba eljutni.

Nagyon érdekel az építészet, a szülővárosom, Békéscsaba építészetéről egy könyvem is megjelent.

Önéletrajza URL

Dénes Attila: Csabai házak almanachja. Békéscsaba, 2019. URL

Publikációi URL

Dugonics András (1740-1818)

Forrás a képre kattintva látható.

Ebben a lexikonban Dugonics András a “kakukktojás” Matematikus egyetemi tanár volt, és szegedi, de az ő idejében még csak Nagyszombatban és Budán lehetett egyetemi tanár. A magyar matematika történetében azonban fontos szerepet játszott. Meg sok más egyéb – pl. irodalmi – területen is.

A Szegedi Tudományegyetem központi épülete a Róla elnevezett téren áll.

Dugonics András Wikipédia URL

Dugonics András életrajza URL

Egerváry Jenő (1891-1958)

Forrás a képre kattintva látható.

(Debrecen, 1891. április 16. – Budapest, 1958. november 30.)

Egerváry Béla és Madarassy Ilona fia. Középiskolai tanulmányait a debreceni Állami Főreáliskolában  (1901–1909) végezte. 1914-ben a budapesti tudományegyetemen bölcsészdoktori oklevelet szerzett. 

1914-1917-ben az egyetem földrengési obszervatóriumban tanársegéd, 1918-tól a Budapesten a felső ipariskola tanára. 1922-1927-ben a szegedi egyetemen Az analízis és alkalmazása c. tárgykör magántanára.  A Szegedi tudományegyetemről 1927-ben politikai okokból távolították el. Erre az 1919-es Tanácsköztársaság idején tanúsított magatartása (előadásokat tartott az egyetemen) adott okot: magántanári képesítését visszavonták.  Karrierje azonban nem ért véget: 1928-tól a budapesti egyetemen Az analízis és annak matematikai-fizikai alkalmazásai c. tárgykör magántanáralett. 1932-ben Kőnig Gyula-díjat kapott.

1938-ban a budapesti egyetemen ismét habilitált Az analízis és annak matematikai alkalmazásai” témakörből. 1938-tól a budapesti Tudományegyetem magántanára. 1941-ben nevezték ki a Műegyetem nyilvános rendes tanárává, a II. számú Matematika Tanszék tanszékvezetője lett. 1952-től 1958. október 15-i nyugdíjaztatásáig a Budapesti Műszaki Egyetem Építőipari és Közlekedési Kara Matematika Tanszékének a tanszékvezetője. Tanított az ELTE-n is.1947-ben megalapította az MTA Alkalmazott Matematika Kutató Intézetét. A Tudományos Tanács elnökévé Egerváry Jenőt nevezték ki, aki a Mechanikai és Szilárdságtani Osztályt, majd a Matematikai Kutató Intézet átszervezése után a Mátrixelméleti és Alkalmazási Osztályt vezette.

A Magyar Tudományos Akadémia tagja (levelező 1943-ban, rendes tag: 1946-ban.)

1952-1958 októberéig oktatási igazgató az építőmérnöki (és közlekedési) műszaki egyetemen, a matematika tanszék tanszékvezető egyetemi tanára.1949-ben és 1953-ban Kossuth díjat kapott.

Életének egy kritikus pillanatában összeomlott, 1958. november 30-án öngyilkos lett. Halálának tragikus körülményeiről a következőt olvashatjuk: „Egy soha meg nem bocsátható és helyre nem hozható félreértés Egerváry professzort olyan ügybe keverte, amelyben alapvető ártatlansága bizonyára hamar kiderült volna. A méltatlan és megalázó helyzetet e talpig férfi nem tudta elviselni, és önkezével vetett véget életének” (Kurutzné Kovács Márta: Szabó János életútja, Építés – Építéstudomány 29 (2001) 5-17).

Egyik legjelentősebb eredménye a Kőnig Dénestől származó, utóbb ökonometriában alkalmazást nyert gráfelméleti tétel általánosítása (1931). A Matematikai és Fizikai Lapokban megjelent, a gráfok kombinatorikus tulajdonságairól szóló cikke (amelynek jelentőségét csak húsz évvel később ismerték fel és kezdték alkalmazni az operációkutatásban) lett az alapja a magyar módszer néven ismert algoritmusnak.

Fő kutatási területei a geometria és differenciálegyenletek alkalmazása, főként a differenciálgeometria, a forgórendszerek kritikus szögsebességének megállapítása és a kinetikus gázelmélet alapjai. Élete utolsó éveiben elsősorban a mátrixelmélettel és annak alkalmazásával foglalkozott, eredményei közül különösen jelentősek a függőhidak általános elméletének megalapozására és felépítésére irányuló kutatásai. A Hungaria Acta Mathematica szerkesztője (1946-1949). 

A szellemi teljesítmény mellett hegymászóként szintén jelentős eredményeket ért el. (Tátra-csúcs megmászása, stb.)

https://web.archive.org/web/20041227205125/http://www.fsz.bme.hu/mtsz/mhk/csarnok/e/egervary.htm

KÁNTOR, T.: Biographies, A Panorama of Hungarian Mathematics in the Twentieth Century I. (Ed. J. Horváth) Springer, 2006, 563-607.

RÓZSA Pál: Egerváry Jenő munkásságáról. Matematikai Lapok, IX. (1958) 193- 225.4.

RÓZSA Pál: Egerváry Jenő tudományos munkáinak jegyzéke. Matematikai Lapok, X. (1959) 1 -4 .

Kántor Sándorné Varga Tünde: A magyar módszer megteremtője: Egerváry Jenő (1891-1958) URL

Egerváry Jenő (1891-1958) A Műegyetem professzora URL

Farkas Gyula (1847–1930)

Forrás a képre kattintva látható.

Kisbarnaki Farkas Gyula (Pusztasárosd, 1847. március 28. – Pestszentlőrinc, 1930. december 26.) matematikus, fizikus, a Magyar Tudományos Akadémia rendes tagja. A magyarországi alkalmazott matematika és elméleti fizika jelentős alakja. Egyebek mellett nevéhez fűződik a Carathéodory-elvet is megelőző Farkas-féle entrópiatétel kidolgozása (1895), valamint a lineáris egyenlőtlenségek vizsgálata kapcsán kidolgozott, később a lineáris programozásban is alkalmazott Farkas-lemma (1902). Közel három évtizeden keresztül, 1888 és 1915 között a kolozsvári Ferenc József Tudományegyetem elméleti fizikai tanszékének vezetője volt.

Egy dunántúli elszegényedett nemesi családban született Pusztasárosdon. Apja kisbarnaki Farkas Ferenc (1820-1882) az Esterházy grófok uradalmi jószágigazgatója volt Lepsényen, a család, később Győrbe költözött. Érettségi vizsgáit a győri bencések gimnáziumában tette le, majd 1866-tól jogi tanulmányokat folytatott a Pesti Egyetemen, illetve zenei érdeklődését kielégítendő a Fővárosi Felsőbb Zeneiskola tanulója lett. Előbb zongoratanulmányait adta fel (pedig koncerteket adó zongoraművész volt), majd – többek között az egyetemen fizikát tanító Jedlik Ányos hatására – érdeklődése a jogról a természettudományok felé fordult, ezért hamarosan átiratkozott a bölcsészettudományi karra. Miután szülei tönkrementek, 1870-ben megszakította tanulmányait, és négy évig a székesfehérvári állami főreáliskolában tanított fizikát és kémiát, emellett a Pápai Állami Tanítóképző Intézet tanára volt. 1874 és 1880 között gróf Batthyány Géza alkalmazta gyermekei házitanítójaként, őket elkísérve beutazta Olasz- és Franciaországot. Időközben 1876-ban megszerezte kémia–fizika szakos tanári oklevelét. Miután magántanítványai leérettségiztek, 1880-ban Budapestre költözött 1881-ben pedig mennyiségtanból – melléktárgyakként természettanból és csillagászatból – bölcsészdoktori képesítést is szerzett a Budapesti Tudományegyetemen. 1881-től a fővárosi egyetemen a  komplex függvénytant – korabeli kifejezéssel az imaginárius változók elméletét – oktatta magántanárként. Az 1887-es év fordulópontot jelentett életében. Ez év januárjában a kolozsvári egyetemen a mennyiségtani természettan tanári teendőinek ellátására kapott megbízást, magántanári rangban. E minőségében 1915-ig, nyugdíjba vonulásáig hűséggel szolgálta a kolozsvári egyetemet. 1888 után nyilvános rendes tanári címmel, tanszékvezetőként folytatta oktatótevékenységét és kutatómunkáját. Közel három évtizeden keresztül, 1888 és 1915 között a kolozsvári Ferenc József Tudományegyetem elméleti fizikai tanszékének vezetője volt. 

Több ízben, 1889–1890-ben, 1892–1894-ben, 1896–1899-ben és 1902–1903-ban a matematikai és természettudományi kar dékánja volt, egy tanéven keresztül, 1907–1908-ban pedig az egyetem rektori teendőit is ellátta. Máig ható tudományos munkássága mellett meghatározó szerepet játszott abban, hogy a XX. század első évtizedeire a nemrégen, szinte a semmiből induló kolozsvári Matematikai Intézet egy negyedszázad múltán az Osztrák–Magyar Monarchia legkiválóbb tudományos műhelyei sorába emelkedett. A tudomány iránti elhivatottsága, nagyszerű emberi értékei révén mind tanártársai, mind tanítványai közt nagy tekintélynek örvendett. Befolyását arra használta, hogy az egyetemi oktatás-kutatás anyagi és személyi föltételei a lehető legjobbak legyenek. Egyre súlyosbodó szembetegsége, glaukómája miatt 1915-ben visszavonult katedrájától, Pestszentlőrincre költözött, és kutatásainak szentelte idejét. Itt halt meg 1930. december 26-án.

Az 1870-es években – a külföldön tartózkodó Batthyány családot kísérve – személyes ismeretséget kötött Charles Hermite és Yvon Villarceau francia matematikusokkal. A találkozás ösztönzőleg hatott rá, s pályája első szakaszában főként matematikával foglalkozott, első elméleti munkái francia tudományos folyóiratokban jelentek meg (pl. Comptes Rendus). Behatóan tanulmányozta a gyökközelítő eljárások konvergenciakérdéseit, az elliptikus függvényeket, valamint a lineáris egyenlőtlenségeket. Ez utóbbiak elméleti alapjait Hermann Minkowskitól függetlenül 1902-ben publikálta (Farkas–Minkowski-tétel). A mechanikai egyensúlyelmélet Fourier-módszer szerinti matematikai bizonyítása során jutott el tételének kidolgozásához, s az általa meghatározott függvény, illetve a sorbafejtés segítségével kidolgozta több lineáris egyenletrendszer megoldását. Egyebek mellett nevéhez fűződik a Carathéodory-elvet is megelőző Farkas-féle entrópiatétel kidolgozása (1895), valamint a lineáris egyenlőtlenségek vizsgálata kapcsán kidolgozott, később a lineáris programozásban is alkalmazott Farkas-lemma (1902).  Eredményeinek jelentőségét az 1950-es években ismerte fel két amerikai matematikus, Harold W. Kuhn és Albert W. Tucker, s az általuk továbbfejlesztett Farkas-lemma a lineáris programozás és optimalizáláselmélet egyik alaptétele lett. Matematikai munkásságának további jelentős eredményei közé tartozik, hogy megadta a Bolyai Farkas nevéhez fűződő gyökközelítő eljárás konvergenciakritériumát, általánosította a komplex függvénytan Picard-tételét, valamint Magyarországon az elsők között foglalkozott az iterált függvények elméletével, vektoranalízissel és vektoralgebrával. 

Kolozsvári tevékenységének kezdetén abbahagyta matematikai kutatásait és teljes erővel új feladatának ellátására összpontosított. Tájékozódott, hajlamainak megfelelő kutatási területet keresett. Az egyetem neves kémiaprofesszorának, Fabinyi Rudolfnak a hatására az elméleti fizikát a fizikai kémia felől közelítette meg. Nagy hatást tett rá W. Ostwald “Lehrbuch der allgemeinen Chemie” címû könyvének fizikai-kémiai része, amelyből tudomást szerzett H. Helmholtz termodinamikai vizsgálatairól. Fabinyi Rudolf vizsgálatai a galvánelemek elméletének termodinamikai vonatkozásaira hívták fel Farkas Gyula figyelmét, aki 1887-1888-ban már saját eredményeivel jelentkezett. 1888-ban a termodinamika második főtétele is kezdte foglalkoztatni. A galvánelemek elméletének elektromos vonatkozásai vezettek az elektromos áramlásra és az “elektromágnesi tömegmozgató hatásokra” vonatkozó 1888-92 között végzett vizsgálataihoz. A virtuális mozgások és a mechanika általános egyensúlyi elveinek axiomatikus tanulmányozása, az elektrodinamika és a relativitáselmélet elméletével foglalkozott. Nevéhez fűződik annak az elvnek a megfogalmazása, amellyel – Constantin Carathéodory azonos eredményeit tizennégy évvel megelőzve – az entrópia növekedésének egyik szükséges és elegendő feltételét fektette le 1895-ben. A Farkas-féle elv kimondja, hogy egyetlen termikusan homogén – azaz termodinamikai egyensúlyban lévő – test vagy rendszer sem juttatható hőcsere nélkül lezajló adiabatikus folyamat útján olyan állapotba, amelybe hőcserével járó folyamat, hőközlés során eljuthat. Egyszerűbben: az adiabatikus állapotváltozás visszafordíthatatlan. Ez a termodinamika második főtételét, az anyagi rendszerekben lezajló folyamatok irreverzibilitását igazoló posztulátum az adiabatikus elérhetetlenség elve néven is ismert. A matematikai fizika területén elért további jelentős eredménye volt az egyenlőtlenségek használata a termodinamikai egyensúly kritériumrendszerének vizsgálatára, újszerű matematikai eljárásokat dolgozott ki az Ampère-féle erőtörvény igazolására, a Lorentz-féle transzformációs szabály levezetésére, továbbá olyan irányban bővítette a Maxwell-egyenleteket, hogy azok a hipotetikus mágneses monopólusokra is alkalmazhatóak legyenek. 

Jelentős tevékenységet fejtett ki a matematika és a fizika népszerűsítése, illetve oktatás-módszertani korszerűsítése terén is. Litografált egyetemi jegyzetei mellett már 1872-ben természettudományi népiskolai tankönyvet írt. Kolozsvári professzorként olyan, később jelentős életművű fiatal matematikusokat hívott meg az egyetemre, mint Riesz Frigyes, Fejér Lipót, Schlesinger Lajos és Haar Alfréd. Sokat tett a két Bolyai életművének elismertetéséért is, részben szervezőmunkájának volt köszönhető a Bolyai János kolozsvári szülőházát jelölő emléktábla kihelyezése. A kolozsvári emléktábla és a marosvásárhelyi Bolyai-síremlék avatóbeszédét is ő tartotta. 

Írásai, tanulmányai főként a Magyar Tudományos Akadémia, illetve külföldi tudós társaságok kiadványaiban jelentek meg. 1874-ben a kérészéletű Székesfehérvári Figyelő című hetilap alapító szerkesztője, 1894 után pedig tagja volt a Középiskolai Matematikai és Fizikai Lapok szerkesztőbizottságának. 

Fiatal korában vonzotta a zongoraművészet, több koncertet adott dunántúli városokban és Nizzában, illetve zeneelméleti cikkeket is publikált.

Tudományos érdemei elismeréseképpen 1898-ban a Magyar Tudományos Akadémia levelező, 1914-ben rendes tagjává választották. 1924-től tiszteleti tagja volt az Eötvös Loránd Matematikai és Fizikai Társulatnak – amelynek korábban megalapításában is közreműködött –, emellett kolozsvári évei során, 1892-ben elvállalta az Erdélyi Múzeum-Egyesület természettudományi szakosztályának elnöki feladatait. 1872-ben – népiskolai természettani tankönyve elismeréseként – a Katolikus Néptanítók Székesfehérvári Egylete tiszteleti tagjai sorába választotta. 

Nemzetközi megbecsültségét tanúsítja, hogy az olasz–magyar tudományos kapcsolatok kiépítésében elért érdemeiért tagja lett a Palermói Matematikai Körnek (Circolo Matematico di Palermo), 1892-ben pedig a Padovai Egyetem díszdoktorává avatták. 

 

Életműve tiszteletére a Bolyai János Matematikai Társulat 1973-ban Farkas Gyula-emlékdíjat alapított, amellyel az alkalmazott matematikában kiváló eredményeket elérő ifjú tudósokat díjazzák. 

Farkas egyetemi oktatói munkássága helyszínén, a kolozsvári Babeș–Bolyai Tudományegyetem matematikai és informatikai karán működik a 2001-ben szerveződött Farkas Gyula Egyesület a Matematikáért és az Informatikáért, melynek vállalt feladata a magyar nyelvű oktatás és kutatás fejlesztése. A Farkas Gyula Egyesület és a kolozsvári Radó Ferenc Matematikaművelő Társaság 2006-ban közösen Farkas Gyula-emlékérmét alapított, 

 

Tudtad-e?

Kacsóh Pongrác, a János Vitéz daljáték zeneszerzője 1896-ban Farkas Gyulánál doktorált fizikából.

  • Szinnyei József: Magyar írók élete és munkái III. (Fa–Gwóth). Budapest: Hornyánszky. 1894. URL
  • Természettudományi lexikon II. (D–G). Főszerk. Erdey-Grúz Tibor. Budapest: Akadémiai. 1965. 494. o.
  • Gulyás Pál: Magyar írók élete és munkái VIII. Budapest: Argumentum; (hely nélkül): Magyar Tudományos Akadémia Könyvtára. 1992. 276–277. o. 
  • Magyar életrajzi lexikon I. (A–K). Főszerk. Kenyeres Ágnes. Budapest: Akadémiai. 1967. 468–469. o. URL
  • Magyar tudóslexikon A-tól Zs-ig. Főszerk. Nagy Ferenc. Budapest: Better; MTESZ; OMIKK. 1997. 281–282. o. ISBN 963-85433-5-3
  • Gábos Zoltán: Százötven éve született Farkas Gyula. Természet Világa, CXXVIII. évf. 7. sz. (1997) 290–293. o. URL
  • Magyar nagylexikon VII. (Ed–Fe). Főszerk. Rostás Sándor, Szlávik Tamás. Budapest: Magyar Nagylexikon. 1998. 693. o. ISBN 963-85773-5-5 
  • Magyarország a XX. században IV.: Tudomány – Műszaki és természettudományok. Főszerk. Kollega Tarsoly István. Szekszárd: Babits. 1999. 23., 26., 29., 84. o. URL
  • Új magyar életrajzi lexikon II. (D–Gy). Főszerk. Markó László. Budapest: Magyar Könyvklub. 2001. 515–516. o. ISBN 963-547-414-8 
  • Martinás Katalin: A termodinamika XX. század előtti magyar története. Elérés: 2010. szeptember 9. URL
  • Ortvay Rudolf: Farkas Gyula rendes tag emlékezete. Budapest: Magyar Tudományos Akadémia. 1933. 
  • Filep László: Farkas Gyula élete és munkássága. Matematikai Lapok, (1977 – 1981)
  • Martinás Katalin: Farkas Gyula. Fizikai Szemle, (1992)
  • Tanulmányok Farkas Gyuláról. Fizikai Szemle, (1997)
  • Új utak a magyar operációkutatásban: In memoriam Farkas Gyula. Komlósi Sándor, Szántai Tamás. Pécs: (kiadó nélkül). 1999. 
  • Gaal György: Farkas Gyula, a Kolozsvári Ferenc József Tudományegyetem tanára. Alkalmazott Matematikai Lapok, évf. (2007) 303–318. o.
  • Proceedings of the International Conference in Memoriam Gyula Farkas, August 23-26, 2005. Cluj-Napoca. Edited by Kása, G. Kassay, J. Kolumbán. (hely nélkül): Cluj University Press. 2005. URL
  • Gábos Zoltán – Kolumbán József – Németh Sándor: Farkas Gyula. In Hivatás és tudomány: Az Erdélyi Múzeum-Egyesület kiemelkedő személyiségei. Kovács Kiss Gyöngy. Kolozsvár: EME. 2009. 81–104. o. 
  • A Farkas Gyula-emlékérem alapító okirata. Elérés: 2010. szeptember 9. URL
  • 125 éves a kolozsvári egyetem. Szerk. Cseke Péter és Hauer Melinda. Kolozsvár, Komp-Press Kiadó, 1998.
  • Sziklay János: Dunántúli kulturmunkások. A Dunántúl művelődéstörténete életrajzokban. Bp., Dunántúli Közművelődési Egyesület, 1941.
  • Das geistige Ungarn. Biographisches Lexikon. Hrsg. Oscar von Krücken, Imre Parlagi. Wien-Leipzig, W. Braumüller, 1918.
  • Százhuszonöt éve nyílt meg a Kolozsvári Tudományegyetem. Emlékkönyv. Összeáll. Gazda István. Piliscsaba, Magyar Tudománytörténeti Intézet, 1997.
  • A Magyar Tudományos Akadémia tagjai 1825-2002. Szerzők: Markó László, Burucs Kornélia, Balogh Margit, Hay Diana. Bp., MTA Társadalomkutató Központ, 2003.
  • Magyarok a természettudomány és technika történetében. Főszerk. Nagy Ferenc, Nagy Dénes. Bp., MVSZ-MTA-BME-MTESZ-Országos Műszaki Információs Központ és Könyvtár, 1986.
  • Révai Új Lexikona. Főszerk. Kollega Tarsoly István. Szekszárd, Babits, 1996-.
  • Sain Márton: Matematikatörténeti ABC. 6. kiad. Bp., Nemzeti Tankönyvkiadó-TypoTEX, 1993.
  • Új magyar életrajzi lexikon. Főszerk. Markó László. Bp., Magyar Könyvklub
  • Illés Tibor, Oláh-Gál Róbert: Farkas Gyula nyomában: Szemelvények egy természettudós életéből és tudományos hatásából (magyar nyelven). Érintő (Bolyai János Matematikai Társulat), 2017. június 1. URL
  • Oláh-Gál Róbert: Kacsóh Pongrác, a fizikus. Fizikai Szemle, sz. (2009) URL
  • Farkas Gyula élete és munkássága URL

Fáry István (1922-1984)

Forrás a képre kattintva látható.

(Gyula, 1922. június 22. – El Cerrito, Contra Costa megye, Kalifornia, 1984. november 2.) magyar–amerikai matematikus.

1922-ben Gyulán született, Budapesten végzett, majd Szegeden doktorált 1947-ben, majd elhagyta Magyarországot, és a Sorbonne-on újabb doktori fokozatot szerzett 1955-ben.  A Montreali egyetemre került tanárnak. Kanada után az 1958-ban az USA-ba ment és a Kaliforniai Berkeley Egyetemre került. 1962-ben lett professzor. El Cherrito-ban, otthonában érte a hirtelen halál, 1984-ben, 62 éves korában.

Kutatási területe az algebrai topológia és a geometria. A csomózott térgörbék görbületével kapcsolatban bizonyított be egy fontos tételt, amit ma Fáry–Milnor-tételként ismerünk (1949). Egy másik tétele, a Fáry-tétel (1948) kimondja, hogy a síkbarajzolható gráfok minden esetben kizárólag egyenes szakaszok felhasználásával is megrajzolhatók, tehát a görbe vonalak használata nem eredményezi a lerajzolható síkgráfok nagyobb körét. Az 1950-es években érdeklődése az algebrai topológia felé fordult, élete vége felé pedig az algebrai geometriával kezdett foglalkozni.

  1. S. Chern, J. DeVogelaere, R. C. Kirby: Istvan Fary (angol nyelven). University of California, 1985. (Hozzáférés: 2021. január 13.)

Istvan Fary’s early mathematical work was geometric in nature. His most famous work (in 1949) can be explained to a non-mathematician. It concerns knots, that is, imbeddings of a circle in 3-dimensional space. A knot can be visualized as a tangled piece of rope with the ends tied together. For our purposes, two knotted pieces of rope are considered to be the same knot topologically if we can slide one around (without untying the ends) so that it looks identical to the other. The unknot refers to the round circle. 

A given knot will have curvature at each point on the knot; the curvature is zero if the knot is straight at that point, and the curvature is large if the knot is quite bent at the point (we assume the knot is smoothly turning with no sharp angles). The total curvature of a knot is obtained by summing up (via integration) the local curvatures at each point of the knot. The round unknot (given by the equation x² + y² = 1) has total curvature 2π (corresponding in a sense to the fact that if one makes a full turn, one goes through an angle of 360° or 2π). 

For a curve to be closed, it must have a total curvature greater than or equal to 2π (Fenchel’s theorem). Fary proved that for a closed curve to make a knot it must have a total curvature greater than 4π. 

This theorem combined a hypothesis about the total curvature, which varies as the knot is moved, and a conclusion about the knot, its knottedness, 

― 136 ― 

which is independent of sliding or bending or other motions. Such theorems are relatively rare in mathematics and usually become famous. The theorem was independently proved by John Milnor and has been known as the Fary-Milnor theorem. 

By the mid-1950s, Fary had turned to more algebraic mathematics, specifically algebraic topology. In this subject, one assigns various algebraic structures to topological or geometric objects, and then hopes to understand the objects better by proving theorems about their (supposedly simpler) algebraic structures. This was a very vigorous branch of mathematics and Fary shared in its many successes. 

In the Hungarian tradition, Fary wrote several important papers on the geometry of convex bodies. His activity in recent years was centered around “algebraic stacks” and their possible applications to generalized circuit theory. Fary’s last published paper went in a new direction, with an intriguing mix of probability and geometry. 

Fary’s mathematical career showed great originality and an unusual breadth of mathematics. 

His dream was to share his discoveries in his homeland. After an absence of 36 years, he had been selected by the National Academy of Sciences, USA, to participate in an exchange with mathematicians from Hungary, starting January 1985. However, due to his untimely death, his dream was not realized. 

As a colleague, his expert and broad knowledge of mathematics will be sorely missed, especially in view of the new applications of algebraic geometry to the description of the functioning of the nervous systems of animals. 

As a teacher, Chairman Henkin remarked to one of us that Istvan was among the very best, being at all times concerned with reaching the student’s intellect. He gave them all he could, teaching until his strength gave way three weeks before he died. 

His attitude was always generous, taking people as they are, not as he would have wished them to be and never speaking ill of anyone. 

His greatest love, above Mathematics, was his family; his wife and especially his daughter Kataline. 

  1. S. Chern R. J. DeVogelaere R. C. Kirby

 

Fáry István Wikipédia URL

Fejér Lipót (1880–1959)

Forrás a képre kattintva látható.

Fejér Lipót 1880. február 9-én született, Pécsett, a Szent Mór utca 3. alatti lakásban, Weisz Leopold néven lett anyakönyvezve. Apja Weisz Samu, anyja Goldberger Viktória. A pécsi főreálba járt, ám rosszul teljesített, (a matematika volt leggyengébb tantárgya,) így mikor a felfogadott korrepetitor sem tudott segíteni, apja kivette az iskolából. Ekkor apja üzletében segédkezett. Később mégis folytatta tanulmányait a főreálban, ahol Maksay Zsigmond lett matematikatanára. Maksay nemcsak megszerettette Fejérrel a matematikát, hanem ápolta addig szunnyadó tehetségét is. Ösztönzésére (14 évesen) rendszeres olvasója és feladatmegoldója lett a Középiskolai Matematikai Lapoknak. A lap szerkesztője, Rátz László többször jelezte: „Weisz Lipót megint nagyon szép megoldást küldött.” 1897-ben érettségizett, majd apja nyomására – aki azt szerette volna, hogy Fejérből mérnök legyen, mivel úgy meg tud élni – beiratkozott a Magyar Királyi József Műegyetemre. Itt Kürschák József és Kőnig Gyula előadásait hallgatta. Fél év múlva átiratkozott az egyetem ún. Egyetemes Szakosztályába, ahol matematika–fizika szakos középiskolai tanárképzés folyt. Innen hamarosan a Pázmány Péter Tudományegyetem tanárképző szakára ment át, ahol Eötvös Loránd és Beke Manó voltak tanárai. Harmadik egyetemi évét már Berlinben töltötte, ahol Hermann Amandus Schwarz volt mestere. Schwarz az egyik előadásában azzal az elemi tétellel foglalkozott, miszerint adott hegyesszögű háromszögbe berajzolt háromszögek közül a talpponti háromszög a legkisebb kerületű és ezt a bizonyítást 6 tükrözéssel végezte. Az előadás végén Fejér megmutatta professzorának, hogy ez a bizonyítás 2 tükrözéssel is elérhető. Ugyancsak Schwarz előadásain ismerkedett meg a Fourier-sorok problémájával. Professzora szerint ez megoldhatatlan, ám Fejér nem így gondolta. 1900-ban a Francia Tudományos Akadémia lapjában, a Comptes Rendus-ben tette közé a Fourier-sorok lezártnak hitt elméletének továbbfejlesztéséről, új összegzési eljárásáról szóló tanulmányát (lásd Fejér-tétel). Ez alapozta meg nemzetközi hírnevét, s Henri Poincaré ekkor figyelt fel rá. Ugyanebben az évben (1900-ban) keresztelkedett ki, és változtatta meg nevét Fejér Lipótra. Ez a döntése azt eredményezte, hogy professzora, Schwarz – aki szintén zsidó származású volt – ezt a közös gyökerek megtagadásának vette, s megszakította vele a kapcsolatot. 1902-ben bölcsészdoktori oklevelet szerzett a Fourier-sorok dolgozatával. 

Ezután Göttingenbe ment, ahol David Hilbert előadásait hallgatta. Hazatért, s itthon a Pázmány Péter Tudományegyetemen kapott munkát, mint repetitor (gyakorlatvezető). Fizetést viszont – mivel ez a munka nem számított rendes állásnak – nem kapott, így elfogadta Farkas Gyula, a kolozsvári Ferenc József Tudományegyetem matematikus professzorának felkérését. Kolozsváron az egyetem magántanára, majd 1906-ban adjunktusa lett. 

Bár 1911-ben a kolozsvári egyetem rendes tanárává választotta, mégis, még ebben az évben elfogadta kinevezését a budapesti Pázmány Péter Tudományegyetemre, ahol az egyik Matematikai Tanszék professzora lett. Sokan ellenezték ezt zsidó származása miatt, de végül Eötvös Loránd közbenjárására elfogadták. Fejér élete végéig a budapesti egyetemen tanított, s olyan kiválóságok voltak tanítványai mint Neumann János, Pólya György, Erdős Pál, Turán Pál, Rényi Alfréd, Kalmár László, Riesz Marcell (Riesz Frigyes szintén matematikus testvére) és Lánczos Kornél. 

Számos hazai kitüntetést kapott – köztük a legnagyobb tudományos kitüntetéseket: Corvin-koszorút 1930-ban, majd a Kossuth-díjat 1948-ban és nemzetközi díjakat, valamint elismerést is kapott. 1933-ban a 4 legkiválóbb európai tudós egyikeként meghívták a chicagói világkiállításra. A világkiállítás után 15 amerikai egyetemen tartott nagy sikerű előadás-sorozatot. 

A Bolyai János Matematikai Társulat tiszteletbeli elnöke volt. Tagjai közé választotta őt a Magyar, a Bajor és a Lengyel Tudományos Akadémia, a Calcuttai Matematikai Társaság, díszdoktorrá avatták a budapesti Eötvös Loránd Tudományegyetemen és az amerikai Brown Universityn.

1940-es években számos külföldi állásajánlatot kapott, mivel ki akarták menteni az egyre fenyegetőbb hazai politikai viszonyok közül. Ő azonban még ekkor is ragaszkodott szülőhazájához. Ám a nyilas hatalomátvétel (1944. október 16.) után katedrájától megfosztották, kényszernyugdíjazták, mint a nemzettől idegen elemet. Be kellett vonulnia budapesti gettóba, ahol őt is a Vöröskereszt által védett Tátra utcai házba zsúfolták be. Ez a védettség nem jelenthetett sokat, mivel 1944 karácsonyán, a ház többi lakójával együtt, Fejér Lipótot is besorolták az egyik Duna-parti kivégzésre vezényelt csoportba, de végül is őt egy honvédtiszt kimentette e menetből. Az átélt borzalmak csak ártottak neki. Szellemi képességei saját bevallása szerint romlottak, házát lebombázták, mindene odaveszett. Régi barátai, korábbi tanítványai segítették pénzadományokkal és élelmiszercsomagokkal. Mikor 1950-ben az Eötvös Loránd Tudományegyetemen tiszteletbeli doktorrá avatták, a következőket mondta: „Nagyrészt tanítványaimnak köszönhetem, hogy el nem pusztultam”. 

A sokféle jelzővel elmarasztalt szocialista korszak rendszere alaposan beavatkozott a magyar tudományosságba. Ezt már személyesen megélték közülünk sokan, ki hosszabban, ki rövidebben. A szovjet mintát kellett követni mindenben. Az első lépés volt 1949-ben az MTA átszervezése, politikafüggővé tétele. A tagok egyharmadát kitették, másik kétharmadát elkényeztették és akarva, nem akarva alkalmazkodóvá formálták. Fejér Lipótot megfosztották akadémiai tagságától.

1959. október 15-én hunyt el Budapesten. Halála után Turán Pál két vaskos kötetben tette közzé életművét.

Munkássága a matematika számos területén meghatározó jelentőségű. Kutatásának fő területei: a Fourier-sorok elmélete, az interpoláció- és a függvényelmélet. A Fourier-sorok analízisén kívül jelentős eredményeket ért el a konstruktív függvénytanban (Fejér-interpoláció és mechanikus kvadratúra) és a komplex függvénytanban. A róla elnevezett Fejér-tétel a Fourier-sorok összegezhetőségére vonatkozik. Riesz Frigyessel kidolgozta a konform leképzések alaptételének legrövidebb bizonyítását. Körülötte alakult ki a világhírű Fejér-iskola (Csillag Pál, Egerváry Jenő, Erdős Pál, Fekete Mihály, Kalmár László, Lukács Ferenc, Pólya György, Riesz Marcell, Szász Ottó, Szegő Gábor, Szidon Simon, Turán Pál).

  • Sur les fonctions bornées et integrables. Comptes-Rendus des l’Academie des Sciences, 1900.
  • Vizsgálatok a Fourier-féle sorok köréből. Mat. és Term. tud. Ért., 1902.
  • A folytonos függvények Fourier-féle sorának singularitásairól. Budapest : Franklin, 1910.
  • Hatványsorok többszörösen monoton együtthatósorozattal. Budapest : Franklin, 1936. (Klny. a Magyar Tudományos Akadémia Matematikai és Természettudományi Értesítőjéből.)
  • Approximáció interpoláció útján. Budapest, Akadémiai Ny., 1953. (Approximation durch Interpolation Klny. az Első Magyar Matematikai Kongresszus közleményeiből.)
  • Összegyűjtött munkái. Sajtó alá rend. és jegyz. ell. Turán Pál. Budapest : Akadémiai Kiadó, 1970. 2 db.
  • MTA Marczibányi-jutalma (1911)
  • MTA Marczibányi-nagyjutalma (1918)
  • Corvin-koszorú (1930)
  • Brown University, díszdoktor (1933)
  • Kossuth-díj (1948)
  • Magyar Érdemrend (1950)
  • Tandori Károly: Fejér Lipót. Magyar tudomány, 1980/4. sz. 271–277. pp.
  • Sain Márton: Fejér Lipót. In: Magyar tudóslexikon A-tól Zs-ig. Főszerk. Nagy Ferenc. Budapest: Better; MTESZ; OMIKK. 1997. 285-287. o.
  • Garay Barnabás, Hatvani László, Kolumbán József: Fejér Lipót 100 éve habilitált Kolozsváron stabilitáselméletből, Alkalmazott Matematikai Lapok, 23, 1 (2006) pp. 163–189.
  • Magyar zsidó lexikon. Szerk. Ujvári Péter. Budapest: Magyar Zsidó Lexikon. 1929. 265–266. o. URL
  • Új magyar életrajzi lexikon II. (D–Gy). Főszerk. Markó László. Budapest: Magyar Könyvklub. 2001. 568–569. o. ISBN 963-547-414-8 
  • Czeizel Endre: Matematikusok, gének, rejtélyek, Budapest, Galenus Kiadó, 2011.ISBN 978 963 715 725 7
  • Oláh-Gál Róbert: Villanások Fejér Lipót kolozsvári éveiből, Műszaki Szemle 44 (Historia Scientiarum 5), 2008 URL1 URL2
  • Fejér Lipót (1880-1959) matematikus, Kossuth-díjas akadémikus műveinek és szakcikkeinek bibliográfiája URL
  • 125 éves a kolozsvári egyetem. Szerk. Cseke Péter és Hauer Melinda. Kolozsvár, Komp-Press Kiadó, 1998. 169 [1] o., ill.
  • Sziklay János: Dunántúli kulturmunkások. A Dunántúl művelődéstörténete életrajzokban. Bp., Dunántúli Közművelődési Egyesület, 1941.
  • Gulyás Pál: Magyar írók élete és munkái – új sorozat I–XIX. Budapest: Magyar Könyvtárosok és Levéltárosok Egyesülete. 1939–2002. 
  • Ki-kicsoda? Kortársak lexikona. [Bp.], Béta Irodalmi Rt., [1937].
  • Das geistige Ungarn. Biographisches Lexikon. Hrsg. Oscar von Krücken, Imre Parlagi. Wien-Leipzig, W. Braumüller, 1918.
  • Magyar életrajzi lexikon I-II. Főszerk. Kenyeres Ágnes. Bp., Akadémiai Kiadó, 1967-1969.
  • Magyar Nagylexikon. Főszerk. Élesztős László (1-5. k.), Berényi Gábor (6. k.), Bárány Lászlóné (8-). Bp., Akadémiai Kiadó, 1993-.
  • A Magyar Tudományos Akadémia tagjai 1825-2002. Szerzők: Markó László, Burucs Kornélia, Balogh Margit, Hay Diana. Bp., MTA Társadalomkutató Központ, 2003.
  • Magyarok a természettudomány és technika történetében. Főszerk. Nagy Ferenc, Nagy Dénes. Bp., MVSZ-MTA-BME-MTESZ-Országos Műszaki Információs Központ és Könyvtár, 1986.
  • Magyar tudóslexikon. Főszerk. Nagy Ferenc. Bp., Better-MTESZ-OMIKK, 1997.
  • Don Péter: Magyar zsidó históriák. Anekdota lexikon. Szerk. és életrajzi lexikonnal kieg. Raj Tamás. Bp., Makkabi, 1997.
  • Pécs lexikon. Főszerk. Romváry Ferenc. Pécs, Pécs Lexikon Kulturális Nonprofit Kft., 2010.
  • Révai Új Lexikona. Főszerk. Kollega Tarsoly István. Szekszárd, Babits, 1996-.
  • Sain Márton: Matematikatörténeti ABC. 6. kiad. Bp., Nemzeti Tankönyvkiadó-TypoTEX, 1993.
  • Tolnai új világlexikona. Bp., Tolnai, 1926-1933.
  • Új magyar életrajzi lexikon. Főszerk. Markó László. Bp., Magyar Könyvklub
  • Fejér Lipót Wikipédia URL
  • Vekerdi László: Magyar világ – tudós világ. Budapest. Magyar Tudománytörténeti Intézet, 2011.  p. 106-111.
  • Ács Tibor: 175 éves a Magyar Tudományos Akadémia URL
  • Fejér Lipót a magyar matematikatanítás egyik legnagyobb egyénisége URL
  • Párhuzamos életpályák – Fejér Lipót, Riesz Frigyes (1993) (film) URL

Egyik tanítványa szerint nagyon rövid -egy óránál rövidebb -és nagyon szép előadásokat tartott. Az órák menetét mindig nagyon részletesen előre átgondolta, igyekezett izgalmassá, szinte drámaivá tenni előadásait. Megpróbálta tanítványaival együtt újra átélni egy-egy elmélet keletkezését: óráit úgy építette fel, ahogyan ő a tételek eredeti megalkotását képzelte. Egyéniségét emberi melegség, közvetlenség, humor, önzetlen segítőkészség jellemezte. Széleskörű műveltséggel rendelkezett, tehetségesen zongorázott, szívesen mondott verset. 

Baráti szálak fűzték Ady Endréhez, Balázs Bélához, Babits Mihályhoz, Karinthy Frigyeshez, Ottlik Gézához, Jászi Oszkárhoz, Komjáthy Aladárhoz, Lengyel Menyhérthez, Kisfaludy Stróbl Zsigmondhoz.

 

„Kívülállónak nem lehet elmondani, hogy milyen volt Fejér Lipót. Óriás volt. Földöntúli vigasztalás a puszta lénye. Aki nem ismerte, az valamit nem tud a világról, és sohasem fogja megtudni.” (Ottlik Géza) 

Szabó Péter Gábor írása:

Fejér Lipót (1880–1959) matematikus, a klasszikus matematikai analízis iskolateremtő professzora, a kolozsvári és a budapesti tudományegyetemnek volt nagyhírű tanára. Húszéves korában a Fourier-sorok összegzésére vonatkozó új eljárása a Francia Tudományos Akadémia folyóiratában jelent meg, és lett ennek kapcsán a francia Becsületrend lovagja. Fontos eredményeket ért el a trigonometrikus sorok elméletében, az interpolációelméletben és a konstruktív függvénytanban. Kiváló magyar matematikusok generációit nevelte fel, művésze volt a matematikának. Fejér Lipót kiválóan zongorázott, de nagyon érdekelte a csillagászat is. Fiatalkorában el kellett döntenie, hogy zenész legyen vagy matematikus. Képzőművészeti és irodalmi ismeretei példásak voltak, személyesen ismerték egymást Ady Endrével is. Egyszer Ady egy önmagát ábrázoló, Székely Aladár által készített fényképet adott Fejérnek ezzel a dedikációval: „Fejér Lipótnak, testvéremnek a nagy szenvedésben, a hiábavalóban, mellyel meg akarjuk, meg akarnók mutatni magunkat a világnak s megimádtatni a világgal, melyet néha csaknem úgy lenézünk, mint enmagunkat, — igaz barátja: Ady Endre.” Bár tegyük rögtön hozzá, hogy ez a világnak való megmutatás és megimádtatás távol állt Fejér Lipóttól, akit az őt személyesen ismerők végtelenül szerény embernek mondtak. Van azonban egy másik fénykép is, ahol ráadásul Fejér és Ady együtt láthatók. Ez a felvétel Püspökfürdőn készült, Fejér rá is jegyezte a hátoldalára, hogy „1909. július 23-24. Püspökfürdő Nagyvárad mellett.” Ott vannak a képen látható személyek nevei is: Nagy Mihály, György Ernő, Kanitz Henrik, Ady Endre és Fejér Lipót. Scheiber Sándornak az Irodalomtörténet folyóirat 1960-ban megjelent róluk írt dolgozatában felidézi a jelenlévő Nagy Mihály nagyváradi ügyvéd erről szóló visszaemlékezését. Ekkor Adyt Lukács Hugó gyógyította Kolozsváron. Fejér Lipót Ady Endre és Fejér Lipót „A kolozsvári pihenés mégis jó eredményekkel bíztatott. Ady megerősödve, friss hangulatban sürgette kolozsvári orvosát, hogy engedje át egy kis kirándulásra Nagyváradra. Nagy alkudozások s Ady részéről való komoly szolid fogadkozások után végre megkapta a beleegyezést ahhoz, hogy két napra átránduljon Nagyváradon át a Püspökfürdőbe. Két kolozsvári jó embere kísérte el erre az útra július 25-én azzal a szigorú feladattal, hogy nem tágítanak mellőle, vigyáznak rá, és szépen visszaviszik Kolozsvárra, pihenni. Fejér Lipót, a világhírű matematikus és dr. Kanitz Henrik kolozsvári orvos, tanársegéd voltak kísérői. Emlékszem, hogy kötődött velük. Fejér Lipótot bolondos, gyermekes szeszéllyel és tréfás malíciával azért nyaggatta folyton, hogy matematikai egyenleteket készítsen az utcák görbéiről (latin szót használt).”Fejérnek Adyval való ismeretségéről van azonban egy másik forrásunk is. Kevesen tudják, hogy Fejér fiatalkorában szerelmes volt Harmos Ilonába, aki akkor a Színművészeti Akadémián volt előkészítős növendék. Ilona azonban később nem hozzá ment feleségül, hanem Kosztolányi Dezsőhöz. Fejér egész életében agglegény maradt. Budapesten az MTA Könyvtár Kézirattárában Kosztolányi Dezsőné Harmos Ilona hagyatékában van egy dokumentum, amelyben Kosztolányiné több oldalon keresztül emlékszik vissza Fejér Lipóttal való ismeretségükre. Harmos Ilonának akkor már nem élt az édesapja, a családnak Gödöllőn volt háza, és Fejér is Gödöllőn nyaralt az édesanyjával. „Ilonának, szerelmemnek” – dedikációval nyújtotta át Fejér az értekezését a Fourier-sorokról Harmos Ilonának, aki persze abból egy betűt sem értett. Fejér sok mindenről mesélt neki, a csillagászatról, az Eötvös-ingáról, igyekezett bevezetni Ilonát Verdi, Leoncavallo és Mozart világába,megismertette Goyaval, Raffaelloval, Michelangeloval. Párizsból még két szép metszetet is hozott neki ajándékba. Ilona édesanyja is nagyon azon volt, hogy Fejér felesége legyen, de a lány legszívesebben ezt mondta volna erre: „Menjen hozzá a mama!”. „Fejér leutazott Kolozsvárra, ott tanított az egyetemen, de még több nyarat töltött Gödöllőn… Később Ady Endre és Aczél Ilona is próbáltak felé terelni. Ady egy nem éppen nyomdafestékre való kurta versikét is faragott kettőnk nevére és Gödöllőre, ámbár feltevésének semmi alapja sem volt.” Bár kutattuk, de ezt a verset nem sikerült eddig fellelnünk Ady életművében, persze nem is biztos, hogy megmaradt. Egyébként Fejér még élete végén is nagyon szerette Ilonát, aki ezt írta: „Utoljára a Kútvölgyi kórházban beszéltem vele. Föllármázta az egész folyosót. – Ő az, Ő az, itt van, eljött hozzám az én nagy szerelmem, a Harmos Ilona. – Sírt, zokogott, nyakamba borult. Nagyon fájt érte a szívem.” De hát Kosztolányi még érzékenyebben érintette, emlékszünk Ilona című versére, amely így kezdődik: „Lenge lány, aki sző, holdvilág mosolya: ezt mondja a neved, Ilona, Ilona.” Végezetül még egy levélből idézünk, amelyet eddig nem ismert a tudománytörténet-írás, Kalmár László szegedi matematikaprofesszor hagyatékában találtuk. Péter Rózsa, Kalmár egykori egyetemi évfolyamtársa írta és benne közös professzorukról, Fejér Lipótról is megemlít egy esetet, amely Ady Endrével egy kávéházi találkozásukkor történt: „Meglesték Adyt, aki azt gondolva, hogy senki sem látja, a kávéházi fogasról leemelte és felpróbálta Fejér kalapját. Szörnyen bosszankodott, hogy Fejérnek nagyobb a feje.”

 

A következő anekdotákat szintén Szabó Péter Gábor tanár úr 0107 számú Facebook megosztásából idézem:

 

„Sain Márton személyes emlékei Fejér Lipótról:

 

Sain Márton (1915-1997) neve jólismert a matematika történetét kedvelő hazai olvasóközönség előtt, hiszen ő a szerzője a Nincs királyi út! című nagy kötetnek és a Matematikatörténeti ABC-nek is. Most ez utóbbinak a Fejér Lipótról (1880-1959) szóló szócikkéből idézünk.

“Mint egyetemi tanár lelkesített a lelkesedésével, segítette a kezdőket, ha kellett komoly kritikával, ha úgy adódott megbocsátó

bölcsességgel. Nagy szenvedéllyel tudott vitatkozni, de személyes harag nélkül. Hogy e szerény, de az igazságért kiálló, csendes, de kiabálva vitatkozó, az utcai forgalmat félő, de életét kockára téve, hazájához ragaszkodó tudóst még jobban emberi közelségbe hozzam, szabad legyen megemlítenem, hogy e sorok írója olyan szerencsés volt, hogy tanítványa lehetett. Lebilincselően érdekes előadásain kívül három, személyére vonatkozó élményre emlékszem:

Elsőéves korunkban a Tangl Károly fizikai tanszék nagy előadótermében órakezdésre várakoztunk, a szertári ajtóhoz közel. Egyszercsak az ajtó mögül mind hangosabb és élesebb hangú vita hallatszott. Kissé megrökönyödve ismertük fel Fejér Lipót és Tangl Károly hangját. A kiáltozássá fajult vita végül is hosszú csendben végződött. Kinyílt a szertár ajtaja és láthattuk, amint a kipirult arcú Fejér Lipót szívélyes mosollyal búcsúzott a szintén mosolygó Tangl Károlytól.

Egy alkalommal Fejér Lipót elbeszélte, hogy nagyon szeret háton fekve és a mennyezetet nézve gondolkodni. Bejárónője – amíg meg nem ismerte ezt a szokását – eleinte betegnek vélte. Amikor meggyőződött, hogy betegségről szó sincs, kifakadt: Az egyetemen leadja azt a pár órát. Ha hazajön, akkor lefekszik és a plafont bámulja. Hát mikor dolgozik a Méltóságos úr?

Utolsó Fejér professzor úrra vonatkozó emlékem 1950 tájáról származik. Egy ankét szünetében az idős professzort körülvették régi tanítványai, akik maguk sem tartoztak már a legfiatalabb korosztályba. Megható volt, hogy milyen sok régi tanítványára emlékezett. Egyik őszülő hajú tanárnő megjegyezte: Csak mi, tanítványok öregedtünk meg, de professzor úr semmit nem változott. Fejér Lipót így felelt: Igen, kérem, még fiatalnak érzem magam. A múltkor a körúton, a hátam mögött valaki kiabált: Fiatalúr! Fiatalúr! Én, kérem, hátranéztem, hátha nekem szólt. – A következő nevetés pedig valóban fiatalos volt.”

Fodor Ferenc (1971-)

Forrás a képre kattintva látható.

egyetemi docens, Geometria Tanszék vezetője, a Bolyai Intézet intézetvezetője

A JATE Matematikus szakán szerzett diplomát 1995-ben.

PhD, Auburn University, U.S.A., 1999 (honosítva: SZTE TTK 2002)

Habilitáció, SZTE, 2013.

A véletlenekkel foglalkozó sztochasztikus geometria mellett konvex és diszkrét geometriával, valamint politópok geometriájával is foglalkozik. 

Fodor Ferenc honlapja URL

Újszászi Ilona: A véletlen geometriájáról URL

Fodor Géza (1927-1977)

Forrás a képre kattintva látható.

Fodor Géza (Szeged, 1927. május 6. – Szeged, 1977. szeptember 28.) matematikus, egyetemi tanár, a Magyar Tudományos Akadémia levelező tagja (1973).

 

Édesapja: Fodor József földműves, majd hentesüzletet nyitott, végül húsüzemi munkás, anyja Ács Sánta Ilona. Felesége Velcsov Ilona (1925. nov. 13. Kecskemét) antropológus. Leánya: Fodor Domonka (1954. jan. 23.).

Az Újszegedi Líceumban érettségizett, majd a szegedi Klauzál Gábor Gimnáziumban kiegészítő érettségi vizsgát tett (1945), a Szegedi Tudományegyetemen matematika–fizika szakos tanári oklevelet szerzett (1950), Bekerült a Bolyai Intézetbe gyakornoknak. Nemzetközi hírű mesterei voltak, köztük Rédei László, Kalmár László, Szőkefalvi-Nagy Béla. 

A Szegedi Tudományegyetem, ill. a JATE TTK Bolyai Intézet gyakornoka (1950–1951), a matematikai tudományok kandidátusa (1954), ez után tudományos munkatárs (1954–1958).  1959. szeptember 15-étől kapta meg a docensi rangot, sajátos módon ez után, 1960-ban doktorált. 1967-ben szerezte meg a tudományok doktora fokozatot. 1967. augusztus 1-jétől kapta meg az egyetemi tanári kinevezést. 1971-től A Matematika Alapjai és Számítástudományi Tanszék kettévált, a Számítástudományi Tanszék vezetője Kalmár László maradt, a másik Halmazelméleti és Logikai Tanszék vezetését Fodor Gézára bízták. Az MTA levelező tagja (1973. máj. 11-től).

 A kutatás, az oktatás és a tanszékvezetés mellett 1973–1976-ig a most már József Attiláról elnevezett Tudományegyetem rektori teendőit is Fodor Géza látta el. A JATE tud. rektorhelyettese (1960–1966), az egyetem rektora (1973–1976). Az MTA Matematikai Kutató Intézet Matematikai Logika és Alkalmazásai Osztályának tud. munkatársa (1958–1959). A római Istituto Nazionale per le Applicazioni del Calcolo vendégkutatója (1963–1964). Az MTA–TMB aspiránsa (1951–1954). A Művelődési Minisztérium (MM) Matematikai Szakbizottsága tagja (1963–1969). A Bolyai János Matematikai Társaság tagja (1950-1977)

Szegeden hunyt el, váratlanul fiatalon, a Belvárosi Temetőben nyugszik. Sírját a Nemzeti Emlékhely és Kegyeleti Bizottság védetté nyilvánította (2006-ban).

Az MTA Matematikai Bizottsága tagja (1960–1977). A Szegedi Akadémiai Bizottság, az MTA–TMB Matematikai Szakbizottsága tagja (1967–1973). A Bolyai János Matematikai Társulat elnökségi tagja.

Szocialista Munkáért (1963), Munka Érdemérem (ezüst, 1966).

Tudományos munkássága:

Halmazelmélettel, kéttagú relációk elméletének vizsgálatával, halmazleképzésekkel, ún. transzfinit számok elméletével foglalkozott. Az ún. regresszív függvények elméletének világhírű kutatója. Elsőként bizonyította a regresszív függvények és stacionárius halmazok elméletének alaptételét (amit 1956-tól Fodor-féle alaptételnek is neveznek).

Akadémiai doktori értekezésében a regressziv függvények elméletéről és alkalmazásáról fejtette ki nézeteit. 1973. május 11-én választották be az MTA levelező tagjainak sorába, székfoglaló előadását 1974. április 11-én tartotta meg Vizsgálatok a halmazelmélet köréből címen.

Fodor Géza nevét a kombinatorikus halmazelmélet két jelentős tétele viseli. Ezek egyike a stacionárius halmazok elméletének a kialakulásához vezetett, amelynek olyan nagy előfutárai voltak, mint Alekszandrov és Uriszon, s amely ma már a halmazelmélet abc-jéhez tartozik. A másik Fodor-tétel a halmazleképezések Turán Pál kezdeményezte elméletének egyik alapvető megállapítása: alacsony (végtelen) rendű halmazleképzés értelmezési tartománya előáll független halmazok legfeljebb ugyanolyan alacsony számosságú halmazának egyesítéseként.
Tudományos közleményeit magyar, német és angol nyelven publikálta.

  • Proof of a conjecture of P. Erdős. Acta Scientiarum Mathematicarum, Szeged, 1952.
  • On a problem in the set theory. ASciMathSze, 1954.
  • Generalization of a theorem of Alexandroff and Urysohn. ASciMathSze, 1955.
  • Über transfinite Funktionen I-III. ASciMathSze,, 1960; 1961.
  • On the structure of set mappings and the existence of free sets. Máté Attilával. Ann. Mat. Pura ed Appl., 1964.
  • On a process concerning inaccessible cardinals: I-III. ASciMathSze, 1966-1967.
  • Disjoint systems over set ideals. (On a generalization of the usual conception of almost disjoint set systems.) Máté Attilával. Fund. Math., 1968.
  • Some results concerning regressive functions. Hajnal Andrással. ASciMathSze, 1969.
  • Principal sequence and stacionary sets ASciMathSze, 1973.
  • Leindler László: Fodor Géza. Magyar Tudomány, 1978/4. sz.
  • Csákány Béla – Varga Antal: Matematika. In A Szegedi Tudományegyetem múltja és jelene: 1921-1998 = Past and present of Szeged University. /JATE. Szeged : Officina Ny., 1999. 380-402. p.
  • Szegedi egyetemi almanach : 1921-1995. I. köt. (1996). Szeged, Mészáros Rezső. Fodor Géza lásd 282. p. ISBN 963-482-037-9
  • Fodor Géza Névpont URL
  • Fodor Géza Wikipédia URL

Fodor Géza tartotta nekünk a Matematikai Logika és a Halmazelmélet előadást a hetvenes évek elején. Fiatal egyetemi tanár volt, talán akkor már akadémikus. Erős dohányosként, nem bírta ki, hogy előadás közben ne gyújtson rá. Nagyon nem szerette ezt Lídia néni, a Bolyai Intézet egyik takarítónője, mert a hamu bármikor és bárhova lepotyoghatott, egy dohányos előadó után mindig többet kellett takarí­tani. Rendszeresen szólt is az előadóknak, hogy a tanteremben ne dohányozzanak, csak a szünetben a folyosón, ott volt hamutartó. Amikor Fodor Géza előadása vé­get ért és Lídia néni bement a táblát lemosni, gyorsan rájött, hogy az előadó már megint megszegte a figyelmeztetést: vágni lehetett a füstöt és hamu nyomok min­denütt. Szólt is a professzor úrnak, aki persze mindent tagadott. – De jó lenne egy­szer rajtakapni – gondolta Lídia néni és az ügy érdekében mindent meg is tett. Az előadás alatt a folyóson halkan megközelítette az előadótermet és próbált belesni a kulcslyukon. Ez számára nem is volt olyan egyszerű művelet, mert alacsony terme­te miatt csak lábujjhegyen érte fel a kulcslyukat, másrészt egyik szeme üvegből volt és a vadászat izgalma közben néha eltévesztette, hogy melyikkel kell meglesnie az előadót. Történt egyszer, hogy Fodor Géza, miközben előadását tartotta és az alatt ele­gánsan dohányzott, zajt hallott az ajtó felől. Mintha a kulcslyuk körül matatnának. Gyorsan az ablak felé sétált és a fűtőtest burkoló lemezei közé bedugta a cigarettá­ját. Pár pillanat múlva kivágódott az ajtó, Lídia néni apró termete állt ott és szigorú tekintetébe beleborzongtunk. Tudta mindenki, miért jött. De a professzor úr ártat­lan mosollyal és felemelt kezekkel jelezte, hogy most nincs leleplezés. Egy másik alkalommal azonban majdnem sikerült. Fodor Géza éppen egy nagy slukkot szívott az ablak felé sétálva, de a füstöt kifújni már nem volt ideje, amikor kivágódott az ajtó. Gyorsan eldugta a cigarettát, majd megfordult és feltartott kéz­zel, ártatlan mosollyal jelezte, hogy megint nem sikerült, nincs leleplezés. Lídia néni várt egy kis időt, majd bosszúsan kiment. — Húúúú, ezt megúsztam — szavak kíséretében dőlt ki a füst a professzor úrból.De a sűrű ellenőrzéseket nem lehetett megúszni, tudtuk, hogy egyszer be fog kö­vetkezni a lebukás, akármilyen óvatos is volt az előadónk újabb és újabb trükköket kieszelve. Talán éppen a rágyújtás pillanatát sikerült Lídia néninek elkapnia egy gyors ajtónyitással, de a helyzet egyértelmű volt, tagadni nem lehetett. Nos, akkor megtudhatta mindenki, hogy Lídia néni törékeny alkata mögött milyen hangerő rejlik. Fodor Géza alig állt meg a lábán, olyan letolást kapott. Csak megjegyzem, 1973-1976-ig ő volt a Tudományegyetem rektora. (Dévényi Károly lejegyzése)

Forrás: Szent-Györgyi lovon? Válogatás a Szegedi Tudományegyetem Természettudományi és Informatikai Karának anekdotakincséből / szerk. Szabó Péter Gábor. Szeged, Szegedi Tudományegyetem TTIK, 2014
Fodor Géza karikatúrája kollégáiról. Felső sor: Ádám András, Szendrei János. Alsó sor: Kalmár László, Szőkefalvi-Nagy Béla, Budó Ágoston, Szász Gábor, Moór Arthur, Stachó Lajos és Durszt Endre. (Budó-hagyaték, Klebelsberg Könyvtár gyűjteménye)

Gécseg Ferenc (1939-2014)

Forrás a képre kattintva látható.

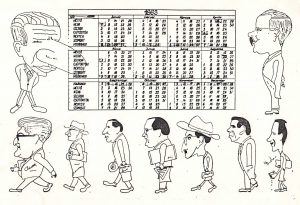
Gécseg Ferenc (Zalavár, 1939. március 13. – Szeged, 2014. október 6.) magyar matematikus, informatikus, egyetemi tanár, a Magyar Tudományos Akadémia rendes tagja. Az automataelmélet és az univerzális algebra neves kutatója, több informatikával kapcsolatos szak elindítója. A szegedi automataelméleti iskola alapítója, számos egyetemi szak bevezetője. 1975 és 1990 között a József Attila Tudományegyetem Számítástudományi Tanszékének vezetője.

 

1957-ben érettségizett a keszthelyi gimnáziumban, majd felvették a Szegedi Tudományegyetem matematika szakára. Itt szerzett középiskolai tanári diplomát (algebra szakosítással) 1962-ben. Ennek megszerzése után az egyetem Bolyai Intézetében kapott gyakornoki, később tanársegédi állást. 1967-ben az egyetem számítástudományi tanszékének alapító tagja lett. 1968-tól adjunktusként, 1970-től egyetemi docensként dolgozott. Bejárta az egyetemi ranglétra fokozatait, 1976-ban akadémiai doktori címet szerzett matematikából, 1977-ben pedig egyetemi tanárrá nevezték ki. 1975-től 1993-ig Kalmár László utódjaként a Számítástudomány Alapjai Tanszék vezetője volt. 1990-ben a tanszék átkerült az egyetem akkor megalakult Informatikai Intézetéhez. Azóta Gécseg Ferenc ebben az intézetben dolgozott, utoljára a Számítógépes Algoritmusok és Mesterséges Intelligencia Tanszék professzoraként. Alapító tagja volt az Informatikai Doktori Iskolának.

  Első kutatási sikereit az univerzális algebrában érte el, majd figyelme az informatikai rendszerek algebrai modelljeinek, az úgynevezett véges automatáknak a kutatása felé fordult. Cikkei számos fontos eredményt tartalmaznak, és új lehetőségeket nyitottak az automaták rendszerei működésének leírásában. Az automaták kompozícióival és dekompozícióival kapcsolatos eredményei fontos szerepet játszanak többek között a digitális hálózatok komplexitásának vizsgálatában. Az 1970-es évek végétől kutatásai a faautomaták és fatranszformátorok elméletére irányultak. Ezen a területen elért eredményei igen jelentősek a gépi fordítás elmélete szempontjából. Három monográfiát, egy tankönyvet és nagyszámú tudományos cikket publikált vezető folyóiratokban és konferencia-kiadványokban.

  Neve az Automaták algebrai elmélete (Algebraic Theory of Automata) című szegedi konferenciasorozat szervezéséhez is köthető, mely az 1970-es évek közepén fontos szerepet játszott a közép-kelet-európai régió és a fejlett nyugati országok tudósai közötti kapcsolatok kiépítésében és fenntartásában. Ezek a kapcsolatok máig hatnak. Sokan csatlakoztak kutatómunkájához Magyarországon és külföldön egyaránt. Oktatói és kutatói hatásának köszönhetően Szegeden létrejött egy nemzetközileg is elismert automataelméleti iskola. Több volt tanítványa ma már vezető oktatóként, illetve professzorként dolgozik. Tudományos munkája elismeréseként 1987-ben a Magyar Tudományos Akadémia levelező tagjává, 1994-ben a Finn Tudományos Akadémia külső tagjává, 1995-ben pedig az MTA rendes tagjává választották. 1989-től 1994-ig az Európai Elméleti Számítástudományi Társaság (EATCS) alelnöke volt. Több magyar és külföldi folyóirat szerkesztőbizottságában dolgozott. Rendszeresen kapott meghívásokat nemzetközi konferenciák programbizottságaiba. Az FCT 1981, FCT 1989 és ICALP 1995 konferenciák programbizottságában elnöki tisztet töltött be; ez utóbbi az egyik legrangosabb nemzetközi konferencia a számítástudomány területén. Személyes érdeme, hogy ezek a konferenciák Szegeden kerülhettek megrendezésre.

2009-ben professor emeritusi címet kapott. Három alkalommal volt Finnországban vendégprofesszor: Turkui Egyetem (1974–1975), Tamperei Műszaki Egyetem (1978), Finn Tudományos Akadémia (1992–1993).

Az MTA Matematikai Bizottságának, az Informatika- és Számítástudományi Bizottságnak és a Szegedi Akadémiai Bizottságnak lett tagja. 1987-ben megválasztották a Magyar Tudományos Akadémia levelező, 1995-ben pedig rendes tagjává. 1994-ben a Finn Tudományos Akadémia is felvette tagjai sorába. Akadémiai tisztségei mellett a Bolyai János Matematikai Társulat és a Neumann János Számítógép-tudományi Társaság tagja. 1989 és 1998 között az Európai Elméleti Számítógép-tudományi Társaság (European Association for Theoretical Computer Science) alelnöke volt. Számos tudományos szakfolyóirat szerkesztőbizottságába is bekerült: Acta Cybernetica (a tanszékcsoport folyóirata), Foundations of Control Engineering, Journal of General Computer Science, Acta Mathematica és az Alkalmazott Matematikai Lapok.

az automataelmélet, ezen belül az automaták algebrai elmélete és az univerzális algebra.

Jelentős eredményeket ért el az automaták kompozíciójával és dekompozíciójával kapcsolatos problémák kutatása területén. Peák Istvánnal közösen könyvet írt a véges automaták elméletéről, ezzel letéve a számítógép-tudomány automatákra vonatkozó részének fontos alapjait. Foglalkozott a faautomaták kérdésével is, munkatársaival elért eredményeit két könyvben foglalta össze. Az 1980-as években az automaták termékeivel foglalkozott. Szegeden jelentős automataiskolát alapított. Tanszékvezetői időszakában vezették be a programozó–programtervező, illetve 1988-ban a közgazdasági programozómatematikus-képzést. Vezetése alatt kezdődött el Szegeden az informatika szakos tanárok oktatása.

Több mint nyolcvan tudományos publikáció szerzője vagy társszerzője, ebből hét könyv, könyvfejezet, illetve könyvszerkesztés. Munkáit elsősorban magyar és angol nyelven adja közre.

Grünwald Géza-díj (1966), 

Akadémiai Díj (1980), 

Kalmár László-emlékérem (1982), 

Szele Tibor-emlékérem (1990), 

Szent-Györgyi Albert-díj (1995), 

A Magyar Köztársasági Érdemrend középkeresztje (2007)

1.

Amikor az MTA levelező tagja lett, a székfoglaló előadására az egész család elment, beleértve a legkisebb családtagot, 49 éves édesapám akkor még egyetlen unokáját, a hároméves Sanyikát. A családtagok a terem első soraiban foglaltak helyett. Egyikünk sem értett egy szót sem a székfoglaló előadásból, de fegyelmezetten hallgattuk a fejtegetést, és bámultuk az írásvetítőn kivetített bonyolult formulákat. Jó tíz perce tartott már az előadás, amikor az addig csendes Sanyika elunta magát, és ennek hangot is adott: finoman, de azért jól hallhatóan elkezdte a horkolás hangjait imitálni, valahogy így: fűűű-pityipűű, fűűű-pityipűű… Igyekeztünk csitítani, de pár perc múlva újra rákezdte. Családtagok, ismerősök és ismeretlenek, akik a közelében ültünk, halkan kuncogtunk, és próbáltuk visszafojtani a kirobbanni készülő nevetést. Szerencsére édesapám annyira koncentrált az előadására, hogy mindebből semmit nem vett észre…

2.

Az 1974-75-ös tanévet a család Finnországban töltötte, mert édesapám a Turkui Egyetemen oktatott vendégprofesszorként. Én ötödik osztályos voltam akkor, a nővérem pedig hetedikes. Nem jártunk iskolába, hanem édesanyám tanított bennünket minden tantárgyból, kivéve a matematikát, mert azt édesapám vállalta magára. Emlékszem, abban az évben néhány iskolában, így a Ságváriban is az 5. osztályban kísérleti tankönyvet vezettek be matematikából, ami igen nagy ugrást jelentett az akkori általános iskolai matematika-tanításban. Magához a tankönyvhöz nem jutottunk hozzá, mert az abból tanító tanárok is csak a kéziratot kapták meg, de az iskola megküldte édesapámnak a tananyag témaköreit. Az első téma ez volt: „Halmazok”. Semmi magyarázat, hogy ezen belül mégis mit és hogyan kellene tanítani. De ez nem szegte édesapám kedvét, hiszen a kisujjában volt a halmazelmélet. Mint utólag megtudhattam, cicák, nyuszik, almák és körték halmazán keresztül kellett volna tudatosítani magának a halmaznak a fogalmát, és néhány alapvető relációt, mint az „eleme” és a „részhalmaz” reláció, valamint a metszet és az unió fogalmát. Ehhez képest nálunk a következőképpen történt az anyag „elsajátítása”. Leültünk édesapámmal a konyhaasztalhoz, fogott egy darab papírt és egy tollat, majd rajzolt egy kört, bele pedig kis x-eket. Közölte, hogy ez itt a halmaz, ezek pedig az elemei. És így tovább, bevezette a részhalmaz, a metszet és az unió fogalmát. Nekem már itt kezdett ködössé válni az egész. A következő óra azzal kezdődött, hogy két kört rajzolt, bennük adott számú x-ekkel, és vonalak segítségével különféle módon összekötötte egymással a két halmaz elemeit. Közben magyarázta, hogy ezt az egészet hozzárendelésnek nevezzük, ez itt az egyértelmű megfeleltetés, ez meg itt az egy-egyértelmű megfeleltetés. De a megfeleltetést hívhatjuk leképezésnek is. Itt valami filmszakadás állt be nálam. A folytatásra nem emlékszem pontosan, csak arra, hogy félbeszakadtak a matematikaórák, és a tananyagot végül külső segítséggel, a tanévet követő nyári szünetben sajátítottam el, miután hazaértünk Szegedre.

A Magyar Tudományos Akadémia tagjai 1825–2002 I. (A–H). Főszerk. Glatz Ferenc. Budapest: MTA Társadalomkutató Központ. 2003. 400. o.

MTI Ki Kicsoda 2009, Magyar Távirati Iroda Zrt., Budapest 2008, 370. old., ISSN 1787-288X

Adatlap a Magyar Tudományos Akadémia oldalán URL

Csirik János–Horváth Gyula: A szegedi iskoláról, Természet Világa, 2000/II. különszám, 24–26. URL

Egyetemi adatlap életrajzzal és publikációs listával URL

Egyetemi gyászjelentés URL

Elhunyt Gécseg Ferenc matematikus, az MTA rendes tagja URL

Gécseg Ferenc Wikipédia URL

Gécseg Ferenc: Az automataelmélet tündöklése URL

Gehér László (1929-2011)

Forrás a képre kattintva látható.

Matematikus, középiskolai tanár, címzetes egyetemi docens

Zalaegerszegen született, 1929. szeptember 5-én, apja lakatosmester volt. Szülei a helyi Deák Ferenc (ma: Zrínyi Miklós)  gimnáziumba iratták be 1939-ben. Hatodikos gimnazista volt, amikor 1945-ben behívták leventének, elhajtották Németországba, ahol hadifogságba esett, 1946-ban került haza. Az angol hadifogságban matematikatanárokkal volt összezárva, ott szerette meg a matematikát. Korán kitűnt kortársai közül, mint a KÖMAL többszörös díjnyertes feladatmegoldója. (1947-ben és 1948-ban is megnyerte a korosztályos versenyt.)

1949-ben felvették az ELTE matematika-fizika szakára, és az Eötvös kollégiumba. Később azonban – politikai okokból – majdnem eltávolították az egyetemről. (Édesapja 1952-ben nyugatra emigrált, és Amerikába került.) Később is akadtak nehézségei emiatt. Az egyetem elvégzése (1953) után Miskolcra került gimnáziumi tanárnak, ahol 1957-ig dolgozott. Utána került Rényi Alfréd segítségével Budapestre, az Automatizálási Kutató Intézetbe, később (1959) Szőkefalvi professzor mellé az analízis kutatócsoportba, majd – nyugdíjazásáig – a Geometia Tanszékre. Szegeden doktorált, de tudományos előrelépéseit akadályozták bizonyos politikai körök.

Szegeden halt meg, 2011. jún. 10-én.

Varga Antal: Akinek az ereiben is matematika folyik… URL

Polygon,20:2(2012), 1–4.

GEHÉR TANÁR ÚR

Az alábbi történetet Szabó Zoltán geométertől hallottam. Zoli hallgató korában a Gehér tanár úr egy speckolljára járt. Az egyik óra elején a tanár megszólította:- Az óra végén majd jöjjön oda hozzám és megmondom, hogy a mai előadás anyagának hol tudnak utánanézni. Az előadás után persze megfeledkezett róla és Zoli alig tudta utolérni a folyosón.- Tanár úr, tanár úr …- Mit akar?- Tanár úr azt mondta, hogy megmondja, hol találjuk a mai előadás anyagát.- Ezt? Ezt sehol, most találtam ki. (Fülöp Zoltán)

DIFFERENCIÁLEGYENLET

Két ember fölkereste Szőkefalvi-Nagy Bélát, hogy segítsen nekik megoldani egy differenciálegyenlet, ami a munkájukhoz fontos lenne. Szőkefalvi egy darabig nézte az egyenletet, de nem volt ötlete, majd megszólalt: Mutassák meg Gehér László­nak, ha 5 perc alatt nem tudja megoldani, akkor valószínűleg nem is lehet megoldani. (Máté Eörs)

(Forrás: Szent-Györgyi lovon? Válogatás a Szegedi Tudományegyetem Természettudományi és Informatikai Karának anekdotakincséből / szerk. Szabó Péter Gábor.. Szeged, Szegedi Tudományegyetem TTIK, 2014.)

 

Surányi János mesélte róla (aki akkoriban a KÖMAL szerkesztője és a feladatmegoldó verseny egyik szervezője volt): a verseny eredményeinek összesítésekor feltűnt neki, hogy a díjazásra javasoltak között nem látja az akkor már jól ismert feladatmegoldó, Gehér László nevét. Kérdezte a többieket, hogy nem találkoztak-e a dolgozatával. Némi keresgélés után előkerült a dolgozat: a javító tanár félredobta, nem vette komolyan, mert nem volt benne sem egy szám, sem képletek, vagy levezetés. Csak pár sor írás. Jobban megnézve a megoldás pimaszul egyszerű és elegáns volt, ő kapta az első díjat. (Varga Antal)

 

A rendszerváltoztatás előtt a legalacsonyabb tudományos fokozat az egyetemi doktori cím volt. Ezt követte a tudományok kandidátusa, majd a tudományok doktora minősítés. Az egyetemi doktori címet az egyetemeken lehetett megszerezni, az utóbbi kettőt a Tudományos Minősítő Bizottság nevű országos szervezetnél. Az egyetemi doktori címért doktori szigorlatot kellett tenni abból a tárgykörből, amelyhez a jelölt disszertációjának témája tartozott. Analízisből mindig Szőkefalvi-Nagy Béla professzor úr vizsgáztatott. Ezeket a szigorlatokat ő fontos intézeti eseménynek tekintette és meginvitálta rá az Analízis tanszék oktatóit. Ő ezt a vizsgát is abban a stílusban vezette, hogy folyamatosan kérdéseket tett fel a szigorlónak. Tudtuk, a professzor úr mindig gondoskodik arról, hogy bármennyire okos is a jelölt, azért ne bízhassa el magát nagyon, ezért a szigorlat mindig úgy ért véget, hogy a legutolsó kérdésnél a vizsgázó „már nem tudott brillírozni”. Persze, ha a jelölt addig jól szerepelt, ettől függetlenül „summa cum laude”-t adott a szigorlatra.

Gehér László, aki a professzor úr tanítványa volt a Bolyai Intézetben, egy kiemelkedően okos matematikus volt. Ez a doktori szigorlatán is bebizonyosodott. Minden kérdésre kiválóan és kimerítően válaszolt. A vizsga már egy órája tartott, amire korábban nem volt példa. A professzor úr megkérdezte a Fredholm-alternatívát, amit közismerten nehéz volt neki úgy elmondani, hogy elégedett legyen vele. Gehér László mindent tudott ebből is. Ekkor a professzor úr megkérdezte: „És mi volt Fredholm keresztneve?” Ezt Gehér László nem tudta. „Érdemes megjegyezni: Ivar Fredholm-nak hívták. Na mindegy, azért rendben volt a felelet. Summa cum laude.” És mindenki megnyugodott, véget ért a szigorlat. (Hatvani László lejegyzése)

Gévay Gábor (1952-)

Forrás a képre kattintva látható.

Az életpályám messze nem tipikus, tekintettel arra, hogy vegyész diplomával, fizikai kutatóintézetekben végzett több évi munka után köteleztem el magamat a matematikai kutatás mellett. A középiskolában (Kossuth Lajos Gimnázium, Mosonmagyaróvár) még egyformán erősen érdekelt a kémia, fizika és matematika. Talán kitűnő kémia tanárom, László Lászlóné hatására döntöttem úgy, hogy vegyész diplomát szerzek.

1977-ben végeztem Debrecenben, akkori nevén a Kossuth Lajos Tudományegyetemen. A krisztallográfia iránti érdeklődésem végigkísérte az egyetemi éveimet (bár ilyen tárgyunk a hivatalos tantervben csak a legelső félévben volt), így végzés után Budapesten, az MTA Kristályfizikai Kutató Laboratóriumában kezdtem dolgozni, ahol kristálynövesztéssel foglalkoztam. Ez tipikusan interdiszciplináris terület, itt fizikusok, kémikusok, elektromérnökök dolgoztak együtt (fontosságát mutatja – egyebek között –, hogy űrhajósunk, Farkas Bertalan is végzett ilyen irányú kísérleteket az űrben). Számomra nagyon szép és izgalmas munka volt (alapvetően kísérleti jellegű), az egyetemi doktori értekezésemet is ebből írtam, amit 1984-ben védtem meg a debreceni egyetemen.

A fizikán belül erősen vonzott az elméleti fizika is – egy ideig úgy gondoltam, hogy ebben az irányban kell továbbhaladnom (időközben az MTA Központi Fizikai Kutató Intézetében is dolgoztam, ahol rendszeresen látogattam elméleti fizikai szemináriumokat). Ehhez azonban sok matematikát kell tanulni, így erre adtam a fejemet. Kitűnő könyvtáraink vannak, ahol kedvemre válogathattam a tengernyi irodalomban, és gyakran jókora könyvhalmokkal a táskámban tértem haza. Ezzel viszont megnyílt előttem egy olyan világ, amely egyre inkább a bűvkörébe vont, és egy idő után már nem volt kétséges, hogy meg fogok maradni ezen a területen.

Az önálló matematikai kutatómunkáig azonban még hátra volt néhány kitérő. 1985-ben Szegedre jöttem, aminek alapvetően családi oka volt: a nősülésem. Ugyanakkor tisztában voltam vele, hogy ez szakmai szempontból is jó választás, hiszen közismert volt, hogy a szegedi Bolyai Intézet a hazai matematikai kutatás nemzetközi hírű központja. 1991-ben, néhány vargabetű után kerültem a Bolyai Intézet Geometria Tanszékére. Előtte az egyetem más tanszékein is dolgoztam, úgymint a Kísérleti Fizika Tanszék, Ásványtani, Geokémiai és Kőzettani Tanszék, ahol fizikai tárgyakat, illetve kristálytant tanítottam.

Kezdő lévén ezen a területen, nagyra értékeltem minden olyan pozitív impulzust, amely megerősített abban, hogy jó úton járok. Egy ilyenre példa az az ismertetés, amelyet rögtön a legelső matematikai dolgozatomról írt a „Mathematical Reviews” c. referáló folyóiratban Coxeter (aki a 20. századi geometriai kutatások egyik világviszonylatban kiemelkedő alakja volt). Ebben így kezdi egyik mondatát: „The author has the clever idea […]”. Ennek azért is nagyon örültem, mert Coxeter azon szerzők egyike, akinek a könyveit és cikkeit nagy gonddal tanulmányoztam, és ennél fogva egy bizonyos értelemben mesteremnek is tekintettem (és tekintem ma is).

Szerencsémre, a közelebbi, egyetemi környezetemben is támogatókra találtam. E tekintetben hálával említhetem mindenekelőtt Csákány Béla professzort, aki Szegedre jövetelem idején az Algebra és Számelmélet Tanszék vezetője, és egyúttal az egyetem rektora is volt. Tudomása volt matematikai érdeklődésemről, és kezdettől fogva támogatta abbéli törekvésemet, hogy a Bolyai Intézet munkatársa lehessek. A Geometria Tanszék akkori vezetője pedig Nagy Péter volt, aki nemcsak felvett a tanszékére, hanem nagy empátiával és segítőkészséggel egyengette a tanszéken tett kezdeti lépéseimet az oktatás és kutatás terén. Általában is, mind a Geometria Tanszéken, mind az Intézet egészében, a kollegiális légkör mindenkor nagy segítséget és bátorítást jelentett számomra.

Szorgalmasan látogattam a konferenciákat, és ennek révén hamar kapcsolatba kerültem nemzetközileg elismert matematikusokkal, úgymint Jürgen Bokowski, Jörg M. Wills, és (később) Tomaž Pisanski. A velük való szoros együttműködés jelentette – formális értelemben diplomám nem lévén – az igazi felsőfokú tanulmányaimat matematikából (természetesen, a korábban már említett önképzésem során olvasott könyvekkel együtt).

Az említett kitűnő kollégákkal való munkát az is megkönnyíti, hogy mindnyájan fontosnak tartjuk a geometria szemléletes oldalát. A geometria szemléletes, illetve absztrakt oldala régóta vita tárgya, és itt-ott megosztja a művelőit is. A szigorú szembeállításnak persze nem sok értelme van – ez a tanulság adódik abból is, ha a legnagyobbak munkásságát nézzük. David Hilbert pl. egyik nevezetes könyvének ezt a címet adta: „Anschauliche Geometrie” (magyarul: „Szemléletes geometria”); ugyanakkor ő az, aki a 19. század végén az euklideszi geometriát modern, axiomatikus alapokra helyezte (és ezzel a lehető legabsztraktabb megközelítését adta a geometriának). Én magam nemcsak a kutatói, de az oktatói munkámban is mindig igyekeztem hasznosítani a geometria szemléletes oldalát.

Egy másik elv, ami végigkísérte nemcsak a geometria terén, hanem a korábban végzett kutatómunkámat is, a szimmetria. Közhely, hogy a szimmetria szinte mindenütt föllelhető, a természetben és az emberi kultúrában egyaránt. A matematika sem kivétel ez alól (itt persze egzakt formális elmélet – a csoportelmélet – keretében jelenik meg). (A krisztallográfiának is egyik központi elve, mind elméleti, mind gyakorlati szempontból – elegendő itt a kristályok ősidőktől fogva csodált szimmetrikus megjelenésére utalni.) Így adódott, hogy a Nemzetközi Szimmetria Egyesületnek (ISA: International Symmetry Association) is elnökségi tagja vagyok, és ennek keretében több nemzetközi szimmetria konferencia résztvevője, illetve részben szervezője voltam.

Egyik könyvében Coxeter idézi egy másik nagy brit matematikus, Hardy egyik megállapítását: „A matematikus – miként a festő vagy a költő – mintákat alkot. Ha ezek időtállóbbak, annak oka, hogy gondolatokból állnak.” A matematikai mintázatok belső logikai szépsége mellett olykor megjelenik a jól szemléltethető, vizuális szépség is. Ez vezetett oda, hogy a 2000-es évek elején, egyfajta hobbiként, „matematikai művészettel” kezdtem foglalkozni, ami azt jelentette, hogy matematikai formulákkal leírt, számítógép segítségével megjelenített grafikák létrehozásában leltem örömömet. Ebben is partnerekre találtam, így néhány kollégával összefogva, több közös kiállításunk is volt, először a szegedi egyetemen, majd az ország több pontján, és egy alkalommal a berlini Műszaki Főiskolán is.

Néhány éve pedig egy nagyon érdekes, teljesen másfajta szabadidős tevékenységbe kezdtem: ez a családfakutatás, amelynek során a saját, egészen tág értelemben vett családom sokféle ágát próbálom felderíteni. Ez meglepően sok új ismerettel gazdagított (nemcsak a családtagjaim vonatkozásában). Például a legrégibb olyan ősöm, akiről még adatokat tudtam szerezni (és a leszármazási vonal is dokumentálható), Bosnyák Ambrus, aki a török elleni csatákban jeleskedett. Vitéz harcos lehetett, mert még Tinódi Lantos Sebestyén is megemlíti: „Jámbor hősök közett Bosnyák Amborus vala” (Erdéli Históriának Negyedik Része, 1408. sor). 1551-ben esett el annak a hadjáratnak a során, amelyet a török Temesvár elfoglalására indított.

Néhány éve – hivatalosan – már nyugdíjban vagyok, de a kapcsolatom sem az egyetemmel, sem a tágabb matematikus közösséggel nem szakadt meg: a Bolyai Intézetben óraadó vagyok, és a kisebb oktatói elfoglaltság révén felszabadult időmet a kutatás terén igyekszem hasznosítani. Úgy érzem, még sok dolgom van ezen a téren, és remélem, hogy ebből sikerül is minél többet elvégeznem.

/Saját írása/

Haar Alfréd (1885-1933)

Forrás a képre kattintva látható.
  1. október 11., Budapest -1933. március 16., Szeged

Vallásos zsidó családból származott, apja Haar Ignác (1854–1951) földbirtokos, bornagykereskedő. A fasori evangélikus gimnáziumba járt (ahol egyébként a több Nobel-díjast nevelő Rátz László volt a matematikatanára), végzős gimnazista korában már a Középiskolai Matematikai Lapok munkatársa (1902–1903). 1903-ban érettségizett; A József Műegyetem Vegyészmérnöki Osztályán (1903–1904), a budapesti tudományegyetemen kémia szakon tanult (1904–1905), majd 1905-ben beiratkozott a göttingeni egyetemre. Professzorai között volt Pesten  Eötvös Loránd, Kürschák József (1864–1933), Göttingenben Constantin Carathéodory, David Hilbert (1862–1943), Christian Klein, Ernst Zermelo, és még sok más kiváló és híres tudós. Hilberttel különösen jó volt a kapcsolata. 1909-ben matematika és a matematikai asztronómia tárgykörben magántanári képesítést szerzett (Göttingen: 1909; honosítva: Budapest, 1910). 1909 júniusában Hilbert témavezetésével doktorált (49 oldalas doktori dolgozatában a Sturm-Liouville-féle és a gömbfüggvényekből álló függvényrendszereket vizsgálja, és felfedezi a függvényanalízisben azóta is széles körben használt Haar-féle ortogonális függvényrendszereket), és még az évben az egyetem magántanárává habilitálják. Ez rendkívül figyelemreméltó: a híres Göttingeni egyetemen lett magántanár, friss egyetemi végzettséggel, 24 évesen! 1912-ben rövid ideig a zürichi egyetemen működött, majd Farkas Gyula meghívta a kolozsvári egyetemre. Haar elfogadta az invitálást, hazajött Magyarországra. 1912. április 6-ától kezdve az elemi mennyiségtan nyilvános rendkívüli tanára, 1917. szeptember 10-étől pedig nyilvános rendes tanára. Kiváló előadónak tartották, az előadásokhoz írt saját kezű jegyzetei közül nem egy könyv alakban is megjelent később. 

A trianoni tragédia miatt az egyetemnek el kellett költöznie Kolozsvárról, 1921-től kezdve működése Szegeden folytatódott. Itt kollégájával és barátjával, Riesz Frigyessel Haar megalapította a szegedi egyetem matematikai központját, a hozzátartozó könyvtárral együtt -ezt a kortársak „magyar Göttingen”-nek nevezték. Kutatói és oktatói munkássága mellett különleges menedzseri képességekkel is rendelkezett

1922-ben munkatársaival együtt létrehozta az első külföldön is jelentős magyar matematikai folyóiratot, Acta Universitatis… Stientiarum Mathematicarum címmel.

A Matematikai és Természettudományi Kar dékánja (1922–1923), dékánhelyettese (1923–1924). A Göttingeni (1914-től), a Hamburgi Egyetem vendégprofesszora (1929-től). 

A Hamburgi Egyetemen vendégtanárként ismertette a variációszámításban elért eredményeit (1929-ben).

Nagyságát mutatja, hogy minden általa vizsgált területen tudott maradandót alkotni. Fontos eredményekkel gazdagította az analízis számos fejezetét. A matematikai analízissel és a topologikus csoportok elméletével foglalkozott. Eredményeket ért el az ortogonális függvénysorok és szinguláris integrálok, az analitikus függvények, a parciális differenciálegyenletek, a halmazelmélet, a függvényapproximáció, és a variációszámítás terén. Nemzetközileg is kiemelkedő eredményeket ért el a többváltozós variációproblémák elméletének kutatása terén. 

1929-ben a hamburgi egyetem felkérésére ismertette a variációszámításban elért eredményeit. Alapvető jelentőségű utolsó műve 1933-ban jelent meg A mértékfogalom a folytonos csoportok elméletében címmel. A halmazelméletben sikeresen foglalkozott mind a diszkrét, mind a folytonos csoportok vizsgálatával. Továbbfejlesztette a lineáris egyenlőtlenségek elméletét. A matematikatörténetben nevét több fogalom őrzi: az ortogonális függvénysorok elméletében a “Haar-féle függvényrendszer”, a többszörös integrálok variációs kérdéseiben jelentős “Haar-féle lemma. Az ún. invariáns csoportmértékek létezésének bizonyításával (Haar-mérték és Haar-integrál) a modern matematikai kutatások egyik alapkövét rakta le.

Budapesten (Terézváros, VI. kerület Andrássy út 32.–Nagymező utca 15. [Haggenmacher-palota]), majd Szegeden élt (Horváth Mihály utca 6.) és tevékenykedett, Szegeden hunyt el, 1933. márc. 16-án; az egyetem központi épülete előcsarnokában ravatalozták fel, ahol Riesz Frigyes búcsúztatta (1933. márc. 19-én). A budapesti Kozma utcai Izraelita Temetőben nyugszik, sírját a Nemzeti Emlékhely és Kegyeleti Bizottság védetté nyilvánította (2005-ben).

Meghalt Haar Alfréd professzor (A Délmagyarország munkatársától.’) Csütörtökön este fél 8 órakor a belgyógyászati klinika diagnosztikai osztályán elhunyt dr. Haar Alfréd, a szegedi egyetem matematika-professzora. Halálát mintegy másfél hónapos, kínos betegeskedés előzte meg. Még az elmúlt félév-ben előadott, ebben a félévben azonban nem kezdte meg előadásait, mert súlyos betegsége levette lábáról. Másfél hónapon keresztül küzdöttek a klinikán életéért, de az orvosok tudták, hogy csak élete meghosszabbításáról lehet szó, megmenteni nem lehet. Néhány nap óta orvosai minden órában várták a halál bekövetkezését. Dr. Haar Alfréd, aki szinte az utolsó pillanatig eszméletén volt, maga is tudta, hogy a vég elkerülhetetlen. Az utóbbi időben kezelő-orvosain kívül senkit sem engedett betegágyához. Csütörtökön este azután teljesen kimerült teste végső pihenőre tért. 47 éves volt, a halál élete delén, munkássága virágzásában ragadta el az élők sorából. Dr. Haar Alfrédet, akinek családja nem volt. az egyetem a maga halottjának tekinti és gondoskodik az eltemetéséről. Dr. Schmidt Henrik rektor a halálhír vétele után azonnal intézkedett, hogy pénteken déli 12 órára összeüljön az egyetem tanácsa és megtegye a szükséges intézkedéseket, előkészületeket a temetésre. Haár Alfréd konszolidált életmódú, nemcsak megfontoltan gondolkodó, de mindig megfontoltan cselekvő ember Is volt. Az az alaposság, amely Európa szerte méltányolt tudományos munkásságát jellemezte, megnvilvánult magánélete számtalan aprólékosságában Is. Lassan járt, szinte azt lehetett volna hinni, hogy örökké sétál. Felöltőjének és télikabátjának valamennyi gombja mindig be volt alaposan gombolva, kalapját szabályosan a fejére illesztette s rövid lábaival egyenletesen rótta az uccákat. Nehezen ment nála, de ha felmelegedett, akkor lelkesen kapott a bizalmas eszmecsere ritka alkalmán. Meghitt beszélgetés közben a szemei kedvesen ragyogtak s egész modorában lehetetlen volt meg nem látni valami kedves gyerekes vonást. A matematika mellett egyetlen szenvedélye volt: a zene Mint sok más nagy matematikus, a kamarazene remekeiben mélyedt el. Halála nemcsak a tudománynak és a szegedi egyetemnek, hanem a szegedi társadalomnak is nagy vesztesége. Az elhunyt professzor a göttingai, zürichi és a budapesti egyetemen végezte tanulmányait. A göttingai egyetemen a legnagyobb élő matematikus, Hilbert volt a tanítómestere. A mester és a tanítvány között később sem szakadt meg a kapcsolat. Doktorátusát a göttingai egyetemen szerezte. 1907-ben Hilbert professzor asszisztense lett, 1910-ben a matematika és a matematikai asztronómia magántanárává habilitálták. Tüneményes pályát futott meg. 1911-ben már a zürichi egyetem helyettes tanára, 1912-ben pedig a kolozsvári egyetem rendkívüli tanára lett. 1917-ben lett nyilvános rendes tanár, ugyancsak a kolozsvári egyetemen. Dolgozataiban a variációszámítás és a parciális differenciálegyenletek, továbbá a függvénysorok elméletével foglalkozott. Halála annál inkább súlyos vesztesége a magyar tudományos életnek, mert az elmúlt években Igen nagy lendülettel dolgozott Az elhunyt professzor tagja volt a Tudományos Akadémiának. 

1933 március 18. DÉLMAGYARORSZÁG 

Vasárnap délelőtt az egyetemről búcsúztatják dr. Haár Alfréd professzort Holttestét Budapesten temetik el (A Délmagyarország munkatársától.) Beszámoltunk tegnap dr. Haár Alfréd, a szegedi egyetem európai hirü matematikus professzorának tragikus haláláról. A kiváló tudós, a nagyjelentőségű kutató halála nemcsak az országban, de külföldön is, ahol jól ismerték és becsülték, őszinte részvétet és mély megdöbbenést keltett A professzor az utolsó időben már tisztában ‘ volt azzal, hogy betegsége gyógyíthatatlan, tragikus sorsát megadással viselte. Teljesen rábízta magát kezelőorvosára és barátjára, dr. Purjesz Béla professzorra, akin kivül az lutolsó időben senkivel sem érintkezett. A kiváló tudós az utóbbi hónapokban nagyjelentőségű dolgozatokat készített, amelyet már nem volt módjában közzétenni. Betegsége utolsó napjaiban dr. Riesz Frigyes professzortársának és barátjának akarta ezeket a dolgozatokat átadni azzal, hogy azokat tétesse közzé Göttingában, de szándékában gyorsan bekövetkezett halála megakadályozta. Az egyetem tanácsa pénteken délelőtt 10 óra-kor, dr. Schmidt Henrik rektor elnökletével ülést tartott, hogy a temetés ügyében a szükséges intézkedéseket megtegye. A tanács elhatározta, hogy az elhunyt tudóst saját halottjának tekinti és a temetése felöl intézkedik. Megállapították a temetés részletes programját- Eszerint dr. Haar Alfréd holttestét a központi egyetem előcsarnokában ravatalozzák fel vasárnap délelőtt 11 órakor. A ravatalnál dr. Löw Immánuel főrabbi, felsőházi tag, mond gyászbeszédet Az Egyetem tanácsa és a matematikus kar nevében dr. Farkas Béla professzor, dékán búcsúztatja a holttestet, majd a Tudományos Akadémia nevében dr. Riesz Frigyes mond búcsúztatót, végül dr. Haar Alfréd egyik tanítványa beszél. A szertartás és a búcsúztatás után a koporsót autóra teszik és Budapestre viszik, ahol a rákoskeresztúri temetőben helyezik el. A temetés a rákoskeresztúri temető halottasházából történik hétfőn délelőtt 11 órakor. Pénteken délelőtt Szegedre érkezett az elhalt professzor egyetlen hozzátartozója, nőtestvére, aki az egyetem tanácsával együtt intézkedik a temetés ügyében. Az egyetem a halálesettel kapcsolatban a következő gyászjelentést adta ki: „A Magyar Királyi Ferenc József-Tudományegyetem Rectora és Tanácsa, valamint Mathematikai és Természettudományi Kara szomorúan tudatja, hogy H a a r Alfréd bölcsészetdoktor, a mennyiségtan nyilvános rendes tanára, a mathematikai- és természettudományi karnak az 1923 —23 tanévben dékánja és 1923—24 tanévben pro-dékánja, a Magyar Tudományos Akadémia levelező tagja, a Mathematikai és Fizikai Társulat Választmányi tagja, a „Stella” Csillagászati Egyesület elnöki tanácsának tagja, az Egyetem tudományos közleményei mathematikai részének szerkesztője, a göttingeni egyetemnek volt magántanára, a zürichi egyetemnek volt helyettes tanára és több külföldi tudományos társaság választott tagja, hivatásának áldozott élete 48. és egyetemi tanárságának 21. évében folyó évi március hó 16-án este fél 8 órakor elhunyt s ezzel mély gyászba borította Egyetemünket Boldogult Tanártársunkat folyó hó 19-én vasárnap délelőtt 11 Órakor az Egyetem központi épületének előcsarnokában búcsúztatjuk el és hétfőn, folyó hó 20-án délelőtt fel 12 órakor Budapesten a rákoskeresztúri temető halottas házából kisérjük örök nyugalomra. Emlékét kegyelettel megőrizzük.

 

Riesz Frigyessel közös vörös mészkő emléktáblája Szegeden, a Dóm téren látható (Borsos Miklós alkotása, felavatták: 1970. szept. 26-án). Róla nevezték el a Szegedi Tudományegyetemen a Haar Alfréd-termet. Születésének 100. évfordulóján emlékülést rendeztek tiszteletére (Budapesten, 1985. aug. 11–17-én). Halála után barátja, Móra Ferenc írt róla megemlékezést (“Frédi” címmel, 1933-ban); összegyűjtött műveit Szőkefalvi-Nagy Béla adta ki (1959-ben). 

 

A Mathematikai és Physikai Társaság tagja (1910-től), választmányi tagja (1931–1933). A Stella csillagászati egyesület elnöki tanácsának tagja (1921-től). A Deutsche Mathematiker Vereinigung (1910-től) és a palermói Circolo Matematico r. tagja (1912-től). A Magyar Tudományos Akadémia csak 1931-ben választotta meg levelező tagjának.

Szerkesztés

Az Acta Scientiarum Mathematicarum alapító szerkesztője (Riesz Frigyessel, 1922–1933). 

Délmagyarország cikkek: URL URL

  • Über orthogonale Funktionensysteme. Egy. doktori értekezés. (Göttingen, 1909)
  • Egyszerűen rendezett halmazokról. Kőnig Dénessel. (Mathematikai és Természettudományi Értesítő, 1909)
  • Zur Theorie der Spannungszustände in plastischen und sandartigen Medien. Kármán Tódorral. (Göttinger Nachrichten, 1909)
  • Zur Theorie der orthogonalen Funktionensysteme. 1–2. (Mathematische Annalen, 1910–1911)
  • Egy orthogonális függvényrendszerről. (Mathematikai és Természettudományi Értesítő, 1914)
  • A kettős integrálok variációjáról. (Mathematikai és Természettudományi Értesítő, 1917)
  • Die Minkowskische Geometrie und die Annäherung an stetige Funktionen. (Mathematische Annalen, 1918)
  • A lineáris egyenlőtlenségekről. (Mathematikai és Természettudományi Értesítő, 1918)
  • Bolyai János geometriájának jelentősége az egyetemes tudományban. (Szeged, 1921)
  • Über eine Verallgemeinerung des Du Bois–Reymond’schen Lemmas. (Acta Scientiarum Mathematicarum, 1922)
  • Über die Konvergenz von Funktionenfolgen. (Acta Mathematica Szegediensis, 1923)
  • Über asymptotische Entwicklungen von Funktionen. (Mathematische Annalen, 1926)
  • Über reguläre Variationsprobleme. (Acta Mathematica Szegediensis, 1927)
  • Sur l’unicité des solutions des équations aux dérivées partielles. (Paris, 1928)
  • Über einige Eigenschaften der orthogonalen Funktionensysteme. (Mathematische Zeitschrift, 1929)
  • Über unendliche kommutative Gruppen. (Mathematische Zeitschrift, 1932)
  • A folytonos csoportok elméletéről. Akadémiai székfoglaló is. (Elhangzott: 1932. ápr. 18. megjelent: Mathematikai és Természettudományi Értesítő, 1933) Számelmélet. (Bp., 1934)
  • H. A. összegyűjtött munkái. Gesammelte Arbeiten. Részben német nyelven. Sajtó alá rend. Szőkefalvi-Nagy Béla. (Bp., 1959).
  • Magyar zsidó lexikon. Szerk. Ujvári Péter. (Bp., 1929)
  • Halálhír. (Budapesti Hírlap, 1933. márc. 17.)
  • Rados Gusztáv: H. A. (Akadémiai Értesítő, 1933)
  • A. (Acta Mathematica Szegediensis, 1933)
  • Móra Ferenc: Frédi. (M. F.: Szegedi tulipános láda. Bp., 1964)
  • Szőkefalvi-Nagy Béla: H. A. (Magyar Tudomány, 1985)
  • Szőkefalvi-Nagy Béla: Alfred Haar (1885-1933) Invariant measure of mathematical excellence = A. Haar memorial conference. Amsterdam: North-Holland, 1985. p. 17-24.
  • Vértesi Péter: Matematikánk egyik legnagyobb alakja: H. A. (Természet Világa, 1985)
  • Szénásy Barna: H. A. (Évfordulóink a műszaki és természettudományokban, 1985)
  • Magyarok a természettudomány és technika történetében. Főszerk. Nagy Ferenc és Nagy Dénes. (Bp., 1986)
  • Alfred Haar Memorial Conference. Szerk. Szabados József és Tandori Károly. (Amsterdam–Oxford–New York–Bp., 1987)
  • Habermann Gusztáv: Személyi adattár a szegedi polgár-családok történetéhez. (Szeged, 1992)
  • Sain Márton: Matematikatörténeti ABC. (6. kiad. Bp., 1993)
  • Szegedi egyetemi almanach. 1921–1995. I. köt. (Szeged, 1996)
  • 125 éve nyílt meg a Kolozsvári Tudományegyetem. Emlékkönyv. I–II. köt. Összeáll. Gazda István. (Piliscsaba, 1997)
  • Magyar tudóslexikon. Főszerk. Nagy Ferenc. (Bp., 1997)
  • 125 éves a kolozsvári egyetem. Szerk. Cseke Péter és Hauer Melinda. (Kolozsvár, 1998)
  • Csákány Béla: Móra matematikusai. (Szegedi Műhely, 2000)
  • Zsidó síremlékek Budapesten. Szerk. Haraszti György. (Bp., 2004)
  • Tóth Tamás: A budapesti Rákoskeresztúri Izraelita Temetőben nyugvó jeles személyiségek adattára. (Szeged, 2007)
  • Varga Antal: 75 éve halt meg H. A. (Polygon, 2008)
  • Czeizel Endre: Matematikusok – gének – rejtélyek. A magyar matematikusgéniuszok elemzése. Tusnády Gábor: A vizsgált elméleti matematikusok teljesítményének rövid értelmezése. (Bp., 2011)
  • Diszkrimináció emancipáció – asszimiláció diszkrimináció. Magyarországi egyetemi tanárok életrajzi adattára. 1848–1944. I. Zsidó és zsidó származású egyetemi tanárok. Szerk. Kovács I. Gábor. (Bp., 2012).
  • Haar Alfréd Wikipédia URL
  • Haar Alfréd a „Haar-mérték-adó” matematikus URL

Halála után Móra Ferenc írt róla megemlékezést:

Frédi

Alfréd legnagyobb eredményei közé tartozik a később róla elnevezett mérték fogalma. Eleinte azonban, Neumann megpróbálta Haart elkedvetleníteni, azzal, hogy érzése szerint ilyen mérték nem létezhet. A következő versike Haar eredményét ünnepli: 

Said a mathematician  named Haar,

Von Neumann can’t see very far. 

He missed a great treasure 

They call it Haar measure 

Poor Johnny’s just not up to par.

”Egy Haar nevű matematikus azt mondja, hogy„Neumann nem látott elég messzire,Így elszalasztotta a kincset, amit Haar mértéknek hívnak.  Jancsi, nem ütötte meg a mértéket.” MacTutor

 

Nincs jogom azt mondani, hogy meghitt barátom volt Haar Alfréd. A névjegyét adta le nálam, közös vendéglői asztalnál darvadoztunk egyszer-kétszer, s néhányszor egymásba karoltunk az utcán -ennyi volt az egész külső összetartozandóságunk ebben az életben. Nem tudom, kit szeretett és mit szeretett, kiért lelkesedett és miért haragudott; még arról is csak hallomásból tudok, hogy ideges ember volt, és nagyon ki tudott jönni a sodrából. Én mindig csak mosolygósnak láttam -igaz, hogy a mosolygása valami megfoghatatlanul finom szomorúsággal volt beszegve, mint némelyik gloxiniának a piros bársonya fehér csíkkal. Virágban sok van ilyen, ezeket szokták bájosnak mondani, fél hozzájuk érni az ember, hogy a simogatással is kárt ne tegyen bennük: emberben, különösen férfiember kevés. A matematika szegedi professzora ilyen volt. Valahol társaságban találkoztunk először, affajta idegen-összeszoktató vacsorán, amitől már reggeltől kezdve fázik az ember. Mindenki odaült, ahová akart, s mind a ketten az asztal végére igyekezvén, egymás mellé kerültünk. Ej, de kedves arcú, csinos, tiszta fiú -örültem neki, s csodálkoztam rajta, hogy így elhúzódott az asszonyok elől. Ugyan nem is azon, hogy ő is a kopáron kötött ki, hanem hogy az asszonyok engedték menekülni. A nevét természetesen nem értettem, de azzal se sokra mentem volna, ha megértem, mert azelőtt soha nem hallottam. Annyit tudtam, hogy csupa egyetemi emberek ülnek az asztalnál, s úgy gondoltam, hogy a fiú tanársegéd lehet valamelyik fakultáson. Az asztalon szamovár zubogott, valahogy kimondtuk Dosztojevszkij nevét, s a szomszédom már idézte is A kegyelmű-t.-Most olvasod -kérdeztem egy kicsit meglepetve.-Nem, most a Batualá-t olvasom -mosolygott.

Ezen nem csodálkoztam, mert én is akkoriban olvastam. Divat volt akkor ezt a néger regényt olvasni. Énszerintem nem nagyon indokolt divat. Banálisnak tartottam, és valami idézettel igazoltam magam. Ő kijavította az idézetet, és kiderült, hogy amit én öt sornak tudtam, az három oldal. Persze, ő franciában olvasta a regényt, én meg magyar fordításban. Aztán Guido da Verona került szóba meg Jacobsen. Apuleius és Pontoppidan, s ő mindnyájáról úgy beszélt, mintha vacsora előtt tette volna le a kezéből, mint speciális stúdiumot. Most már aztán mégiscsak meg kellett tőle kérdeznem: – Milyen szakos vagy te tulajdonképpen? – Matematikus -nevette el magát. Nekem minden imponál, amihez nem értek, de annyira semmi se, mint a matematika, mert ezen a téren nem ismerek nálam nagyobb antitalentumot. Úgy néztem a „fiú”-ra, mint Archimedészre, pedig még akkor nem is tudtam, hogy Haar Alfréd a neve, s hogy ennek a névnek a pétervári akadémián csakolyan becsülete van, mint a londonin. Csak annyit mondtam neki, hogy ő a második matematikus, aki engem ámulatba ejtett. – Hát az első ki volt?-Katona Dienes.  Azt mondta, nem ismeri. Nem hát, hiszen én se ismertem. Szegedi piarista volt, s innen-onnan száz esztendeje lesz, hogy elaludt az Úrban. –  Akkor mivel ejtett ámulatba? – Azzal, hogy ő volt a világon az egyetlen ember, akinek sikerült meghámoznia szöget. – Nem értem – szólt rám a Frédi gyerekszeme. Nem is érthette, mert ez könyvtári tréfa volt, A matematikának egyik sokat hánytorgatott problémája a trisectioanguli, a szög három részre osztása, aminek én csak a nevét tudom, de hogy a lényege micsoda, arról fogalmam sincs. Dienes atya azt állította, hogy ő megoldotta a problémát, s írt is róla egy könyvet, aminek ezt a címet adta: A szög meghármozása, s ebből csinált a nyomda szöghámozást. Ettől fogva aztán ha találkoztunk Frédivel, mindig „hámoztuk a szöget”. Így hívtuk a beszélgetéseinket, amiknek színhelye rendesen a pesti utca volt. Itthon Szegeden sohase értünk rá kibeszélgetni magunkat -inkább az én hibámból, mint az övéből, mert ő sohase sietett, hanem ha Pesten összeakadtunk, alig tudtunk megválni egymástól. Ösztön volt-e, mi volt-e, de elég gyakran egymásba ütődtünk a körúton, anélkül hogy tudta volna egyikünk a másikról, hogy egy levegőt szívunk. Egyszer, két éve lehet, kegyetlen hideg decemberi estén találkoztam vele az Oktogonon. Én Buda felé igyekeztem, ő arról jött.   -Hát te mit csinálsz itt? -karoltam bele. – Vártalak téged –  ölelt meg. -Merre tartasz? Budára? Elkísérlek a hídig. El is kísért, aztán én kísértem vissza az Oktogonig. Este tíztől éjfél után egyig kísértük egymást a molnárszemű csillagok alatt. Könyvekről, asszonyokról, politikáról, közös barátokról beszélgettünk. Pest már elaludt körülöttünk, a mi szavunk is elhalkult. Csodálatosan szikrázóak voltak azon az éjszakán a csillagok, még a Berenice haja nevű csillagcsoport apró csillagai is szétszórt ékkő-halmaz gyanánt villogtak.-  Ott vagy, Frédikém –  mutattam föl az északi égre.-Hogyhogy? -kapta föl a fejét.-  Haar der Berenice  -tréfáltam vele -, én mondjam neked, a csillagásznak?-  Milyen furcsa -mondta komolyan.   -Mi a furcsa?  – Arra gondoltam az elébb, hogy van-e ott is emberi szenvedés. Most olvastam Sir James Jeans könyvét a világűr rejtélyeiről. The mysterious  universe. A könyv egy fotográfiával kezdődik, amely a  Berenice hajá-nak ködfoltját mutatja, a Mount Wilson két és fél méteres nyílású távcsövével felvéve.  – És mit gondol Sir James Jeans?  – Azt mondja, a világűrben az élet céltalan véletlen. – És mit gondolsz te, Frédi? A válasza tréfás volt, de a hangja nem.  -Majd csak a helyszínen tudom meg. De ha megtudom, hírül adom neked, Ferikém…. Megtudja-e, nem-e, hírül adhatja-e, nem-e, ki annak a megmondhatója? De én soha azon az úton végig nem megyek többet úgy, se a Berenice hajára nem nézek anélkül, hogy az oldalamon ne érezném Frédit, aki óriásként járt a számok rejtélyei közt, és egy fiú mosolyával szenvedett az emberek között. (1933)

Hajnal Péter (1961-)

Forrás a képre kattintva látható.

Hódmezővásárhelyen születtem, majd családunk Szegedre költözött. Édesapám matematika tanár volt. (Hajnal Imre) Sose mondott olyat, hogy legyek matematikus, de a családi beszélgetések alatt a jól felépített, meggyőző érvelések, a szórakoztató fejtörők biztos szerepet játszottak abban, hogy a matematika vált a kedvenc tárgyammá. Általános iskolás koromban indult a Kis Matematikusok Baráti Köre. Ez egy hetenkénti, délutáni plusz óra volt, amit élveztem, mindig vártam. Az első országos versenyen második helyezést értem el. A rádió is közvetített róla, a riportban kaptam néhány szót. Teljesen elfelejtettem, de visszahallgatva a riportot a beszámoló egyik információja az volt, hogy a versenyzők kaptak egy üveg cola-t. A szegedi Radnóti Miklós Gimnázium matematika tagozatos osztályába jártam. Osztálytalálkozókon jött elő a történet, hogy egyszer, amikor az óra végén a tanárnő még elmondott egy megoldást és rögtön elhagyta a termet, akkor én kimentem a táblához. Letöröltem az érvelés egy részét. Mindenkinek mondtam, hogy ezt húzzátok át, ez rossz és felírtam a helyes megoldást. Akkor már a magyar matematikai Olimpiai csapat tagja voltam. A londoni olimpián második díjat szereztem. Nagyon szerettem rajzolni is és felmerült, hogy mérnök legyek. Mégis természetes volt, hogy a matematikus szakot válasszam. Az egyetemen kaptam a legnagyobb hatást. Remek tanáraim voltak: Lovász László, Totik Vilmos, Turán György talán a három legmeghatározóbb. Végzés után egy évig Budapesten az ELTE-n és a Rényi Intézetben tanultam. Itt Simonovits Miklós és Szemerédi Endre adta a legtöbb útravalót. Utána Magyarország megnyílt. Amerikai egyetemekről jöttek professzorok, hogy tehetséges diákokat toborozzanak. Én a University of Chicago egyetemre kerültem és elméleti számítógéptudományt tanultam. Babai László és Janos Simon voltak a témavezetőim. Postdoc éveimet az MIT-n, illetve a University of Princeton-ban töltöttem. Itt ismerkedtem meg Füredi Zoltánnal, akivel több jelentős eredményünk született. Mind a mai napig a kombinatorika, algoritmusok és geometria határterülete érdekel legjobban. Ezt kutatom, tanítom. A geometria valószínűleg a rajzolás szeretete miatt áll közel hozzám. Örülök, hogy matematikus lettem. Azt mondhatom, hogy foglalkozásom “fejtörők megoldása”. Egy matematikai problémát először meg kell érteni, a logikáját, mozgatórugóit fel kell ismerni. A megoldás leggyakrabban egy szikra, ötlet, majd egy kis kidolgozás. Az első szikrákat Édesapám csiholta ki. Nem szólt semmit, de utólag úgy érzem arcára kiült a büszkeség. Én is örülök, ha azt látom, hogy a fiatalok is szeretnek az agyukkal dolgozni. A világ több helyén ott vannak a szegedi diákjaim, akik egyetemünkön szerezték meg a matematikai alapokat. Szabadidőmben olvasok, illetve egy kis gyógynövényes kertet ápolok.

/Saját írása/

Weblapja URL

Édesapja Hajnal Imre Wikipédia URL

Hatvani László (1943-)

Forrás a képre kattintva látható.

Hatvani László (Csongrád, 1943. január 29. –) Széchenyi-díjas magyar matematikus, egyetemi tanár, a Magyar Tudományos Akadémia rendes tagja. A differenciálegyenletek elméleti problémáinak és gyakorlati alkalmazásainak neves kutatója. 1990 és 1992 között a József Attila Tudományegyetem (2000-től Szegedi Tudományegyetem) Természettudományi Kar dékánja, 1996 és 1999 között az egyetem Bolyai Intézete igazgatója.

Életrajza: 

Általános és középiskolai tanulmányait Csongrádon végezte. A Csongrádi Batsányi János Gimnáziumban humán tagozatra járt. Főleg magyar-tanára és osztályfőnöke, a legendás hírű Dr. Fehér Ede hatására a nyelvek és az irodalom érdekelték. Aktív tagja volt az iskola önképzőkörének és a városi amatőr színjátszó társulatnak is; szavalataival gyakran lépett fel iskolai és városi rendezvényeken. Valószínűleg ennek köszönhető, hogy bölcsész pályára készült: úgy tervezte, a Szegedi Egyetemre iratkozik be magyar-latin szakra. A gimnáziumi évek vége felé találkozott olyan egykori iskolatársaival, akik a bölcsészkarra jártak, akiktől úgy hallotta, hogy ott nagyon sokat kell magolni, amit soha nem szeretett. Ekkor fordult érdeklődése a matematika és a fizika felé. Mindig szerette ezeket a tárgyakat már csak azért is, mert ezek elsajátításához elegendő volt ott lenni az iskolai órákon, ott minden ráragadt, amit tudni kellett. Rendhagyó módon, édesanyja korai halála miatt, csongrádi lakosként bentlakója volt diákjai számára fenntartott kollégiumnak, és itt sokszor el kellett magyaráznia az anyagot ezekből a tárgyakból társainak. Ekkor érzett rá először a tanításnak, az ismeretátadásnak kellemes ízére. Ennek lett az eredménye, hogy végül is a Szegedi Tudományegyetem matematika-fizika tanári szakára iratkozott be.

Az egyetemi évek nagy változásokat hoztak az életében. A szigorú házirend által szabályozott kollégiumi élet után rászakadt a mámorító, de azért kicsit ijesztő teljes szabadsággal járó felnőtt kor. Ez teszi széppé az egyetemi éveket, mert ekkor még, a családalapítás időszaka előtt ezt a felnőtt függetlenséget és szabadságot nem befolyásolják a család iránt érzett felelősség korlátai. Óriási élmény volt a tudománnyal való találkozás is az egyetemi foglalkozásokon. Feltárult előtte a matematika csodálatos világa a maga szigorú rendet teremtő szabályaival. Kiváló tanárai voltak, közöttük Szőkefalvi-Nagy Béla, Kalmár László, Tandori Károly, hogy csak a legkiválóbbakat említsük. Új és kijózanító volt az a felismerés, hogy csöbörből vödörbe került, mert nem csak a bölcsészetet, de a matematikát is kemény kitartást kívánó munkával tanulni kell. Megszerette a mindig új élményeket hozó tanulást, a vizsgákra való felkészülést, még magukat a vizsgákat is, ahol a hallgatót örömmel tölti el, hogy számot adhat tudásával őt oktató tanárának, akinek láthatóan szintén örömöt jelent látni munkája eredményét.

Az 1960-as évek elején a matematikus-képzés még abban a rendszerben folyt, hogy matematikus szakon csak harmad- negyed- és ötödév volt. A másodévet elvégző matematika-fizika szakos tanárjelöltek jelentkezhettek matematikus szakra, és a 10 legkiválóbbnak megengedték, hogy leadják a fizika-szakot és matematikus hallgatóként folytassák tanulmányaikat. Ezen a szakon kezdődött el Magyarországon a számítógépek programozását végző szakemberek képzése. Ez további forradalmian új ismeretekkel való találkozást jelentett. Az évek haladtával azért kiderült, hogy érdeklődését mégis a klasszikus elméleti matematika problémái vonzzák leginkább. Negyedéves korában diákköri tevékenység keretében Pintér Lajos tanár úr mentorálásával elkezdett differenciálegyenletekkel foglalkozni. Ez egy újabb mérföldkő volt tudományos fejlődésében. Ekkor kóstolt bele abba, mit jelent a kötelező egyetemi tananyag elsajátításán túlmutató önálló kutatómunka, ami azután kitöltötte egész további életét. Kiderült számára, hogy ez az ember egész életét kitöltő önálló életforma az újabb és újabb problémák felmerülésével jelentkező kihívásokkal, az azokkal való birkózás sikereivel és kudarcaival. Harmadéves korától Népköztársasági Ösztöndíjas. Negyedéves korában a Bolyai Intézet ösztöndíjasa lett, amely azt jelentette, hogy az Intézet végzés után állást biztosít számára.

Már egyetemi éveiben belekóstolt másik meghatározó tevékenységébe, az oktatásba. Harmadéves korától az Analízis Tanszék demonstrátora, ami azt jelentette, hogy bevonták a Tanszék oktató munkájába gyakorlatok vetetésére vonatkozó megbízásokkal. Ezzel kezdődött az a másik szenvedély, amely a kutatással együtt kitöltötte egész életét. Viszonylag korán, még adjunktusként bízták meg a Közönséges differenciálegyenletek főkollégium előadásával, amelyet több mint negyven évig végzett a matematikus szakon. Kevéssel később a matematikus szak első két évfolyama egyik legfontosabb alapozó előadásának, az Analízis-nak az előadásába is bevonták, ami rövidesen teljes egészében az ő gondozásába került, és ami szintén nyugdíjba vonulásáig az ő feladata maradt. Szívesen vállalt oktatást nem-matematikus szakokon is, például ő tartotta a közgazdász hallgatóknak a Kalkulus I-II bevezető előadásokat, amelyekhez jegyzetet is írt. Az ő vezetésével jött létre az 1990-es években a Matematikai és Számítástudományi Doktori Iskola.

Általánosan elismert, hogy az alkalmazott matematika legalapvetőbb területe a differenciálegyenletek. Az 1970-es évek elején a differenciálegyenletek oktatásának és kutatásának Magyarországon még nem volt komoly, a tárgy fontosságának megfelelő hagyománya. Ezért a Bolyai Intézet vezető személyiségei tanácsára 1971-ben Moszkvába, a világhírű Moszkvai Állami Lomonoszov Egyetemre (MGU) ment tanulni, ahol négy évig levelező aspiráns volt az Elméleti Mechanika Tanszéken. Az MGU differenciálegyenletekből a világ egyik legjobb centruma volt és az ma is. Mivel egyetemi tanulmányai alatt Szegeden csak a bevezető fizikai kurzusokat végezte el, az Elméleti Mechanika Tanszéken az aspiránsoktól mechanikából megkövetelt rendkívül magas színvonalú elméleti és feladatmegoldó alapozó tudást rövid idő alatt nagyon intenzív munkával pótolni kellett. Ezen időszaknak köszönhető, hogy nyugdíjas éveinek nyugalmát és időbőségét kihasználva megírhatta a Magyarországon első Klasszikus mechanika matematikusoknak című tankönyvet, amely megjelenés előtt áll.

Tudományos és oktatói karrierjének főbb formális állomásai a következők. 1969-ben védte meg egyetemi doktori disszertációját. Diplomájának megszerzése után az egyetem analízis tanszékének munkatársa, tanársegéde lett. 1971-től adjunktusként, 1976-tól egyetemi docensként  dolgozott a tanszéken. 1989-ben egyetemi tanári kinevezést kapott Szegeden. 1990-ben a Természettudományi Kar dékáni tisztével bízták meg, amit két éven keresztül töltött be. 1996-ban megbízták három évre az egyetem Bolyai Intézete (matematikai tanszékcsoport) vezetésével. Közben 1998-ban az analízis tanszék vezetője lett. A tanszéket 2008-ig vezette. 1997 és 2000 között Széchenyi professzori ösztöndíjjal kutatott. Magyarországi munkái mellett a Leuveni Katolikus Egyetem és a Dél-illinois-i Egyetem vendégprofesszora volt.

1975-ben védte meg Moszkvában a matematikai tudomány kandidátusi, 1988-ban Budapesten akadémiai doktori értekezését. Az MTA Matematikai Bizottságának és a Szegedi Akadémiai Bizottságnak lett tagja. 1994 és 1998 között az MTA közgyűlésének képviselője volt, valamint 1995-ben az akadémia elnökségének tagja lett mint doktori képviselő. 1998-ban megválasztották a Magyar Tudományos Akadémia levelező, 2004-ben pedig rendes tagjává. 2002 és 2008 között a Szegedi Akadémiai Bizottság alelnöke volt. Az akadémia Könyv- és Folyóirat-kiadó Bizottságának tagja. Akadémiai tisztségei mellett a Magyar Akkreditációs Bizottság plénumának és a Bolyai János Matematikai Társulatnak tagja. Számos tudományos szakfolyóirat szerkesztőbizottságába is bekerült: Electronic Journal of the Qualitative Theory of Differential Equations (itt társfőszerkesztő), Dynamic Systems and Applications, Dynamics of Continuous, Discrete and Impulsive Systems, Acta Scientiarum Mathematicarum, Periodica Mathematica Hungarica és Acta Mathematica Hungarica.

A felsorolásból kiderül, hogy a sikeres tudományos és oktatási tevékenység mellett aktív szerepet vállalt a szegedi, sőt általánosabban, a magyar tudományos és oktatási közélet vezetésében, irányításában is. A hármas terhelésen túl, amelyek összehangolása karrierjének egyik kiemelkedő érdeme, próbált minél több időt szakítani családjára is. Hétvégeken és a nyári szünidőkben feleségével és Nóra lányával, aki biológuskutató lett, gyakran látogatták a hegyeket és a vizeket. Utóbbiban nagy segítségükre volt felfújható gumi kajakjuk, amellyel bejárták a Tisza és a Maros szép tájait, amit a Balatonra, sőt még a tengerre is magukkal vittek, és amit két unokájuk is nagy örömmel használt nagyapjuk irányításával. A két leány, Marietta (16) és Dóra (14) már gimnazisták, és nagyapjuk evezés helyett matematikából és fizikából irányítgatja őket, már amikor a lovaglásból eredő bokros teendőik ezt lehetővé teszik.

A családi keretek közötti sporttevékenységet kiegészítette a Bolyai Intézetben nagy hagyománynak örvendő sportéletben való részvétel is. A szakszervezet folyamatosan szervezett az egész egyetemet átfogó bajnokságokat asztaliteniszben és kispályás fociban a különböző karok, intézetek, tanszékek között, amelyekben az Intézet mindig több csapattal is indult. Ezeknek a csapatoknak Hatvani László is állandó tagja volt. Sajnos, már középkorúként (előbb kellett volna!) a teniszbe is belekóstolt és ebből igazi hobbi, sőt szenvedély lett, aminek egészen addig hódolt, amíg egészsége engedte. Azért még ma is mindennap kimozdul otthonról: kihasználva Újszeged csodálatos adottságát, jó levegőjét esténként egy órás intenzív skandináv gyalogtúrát tesz.

Fő kutatási területe a differenciálegyenletek elméleti problémái és gyakorlati alkalmazásai.

A differenciálegyenletek megoldásánál elsősorban a minőségi (kvalitatív) úton történő vizsgálattal foglalkozik. Ezen a témakörön belül az úgynevezett nem autonóm rendszereket kutatja. Emellett jelentős eredményeket ért el a parciális stabilitás (részes stabilitás) problémája (itt a Ljubanov-függvények fejlesztése), valamint a változó együtthatójú súrlódási erő fékező hatásának vizsgálata területén. Itt elsősorban az ezekhez szükséges matematikai módszerek kifejlesztését végezte el. Foglalkozik az informatika és a számítástudomány egyes kérdéseivel is.

Hatvani László a differenciálegyenleteket Pintér Lajos – a Bolyai Intézetben a hallgatókkal és tehetséges középiskolásokkal való foglalkozás ikonikus alakja – biztatására kezdte vizsgálni, és a differenciálegyenletek kvalitatív elméletének világviszonylatban is magasan jegyzett iskoláját alapította meg. Amerikai kollégájával, Theodore A. Burtonnel együtt 1998-ban indították el az Electronic Journal of Qualitative Theory of Differential Equations online folyóiratot nemzetközi szerkesztőbizottsággal. 2002-ben végleges választ adott a funkcionál-differenciálegyenletek stabilitáselméletének egy központi problémájára.

 

Több mint száz tudományos publikáció szerzője vagy társszerzője, ebből négy könyv vagy könyvfejezet. Munkáit elsősorban magyar és angol nyelven adja közre.

  • Grünwald Géza-díj (1971)
  • Akadémiai Díj (1996)
  • Szele Tibor-emlékérem (1996)
  • Széchenyi-díj (2001)
  • Klebelsberg Kunó-díj (2004)
  • A Magyar Köztársasági Érdemrend középkeresztje (2007)
  • Magyar Érdemrend középkeresztje a csillaggal polgári tagozat (2018)
  • Szőkefalvi-Nagy Béla díj (2019)
  • Attractivity Theorems for Nonautonomous Systems of Differential Equations (1978)
  • On the Continuation of Solutions (1980)
  • Stability Theorems for Nonautomomous FDE’s (társszerző, 1989)
  • On the Existence of Periodic Solutions (Krisztin Tiborral, 1992)
  • Asymptotic Stability of the Equilibrium of the Damped Oscillator (Totik Vilmossal, 1993)
  • A Necessary and Sufficient Condition for the Asymptotic Stability of the Damped Oscillator (társszerző, 1995)
  • Integral Condition on the Asymptotic Stability for the Damped Linear Oscillator with Small Damping (1996)
  • Differenciálegyenletes modellek a középiskolában (társszerző, 1997)
  • Differenciálegyenletek megoldásának stabilitási tulajdonságai (2000)
  • Kalkulus közgazdászoknak (2006, angolul is)

Címlapképek URL URL

  • A Magyar Tudományos Akadémia tagjai 1825–2002 I. (A–H). Főszerk. Glatz Ferenc. Budapest: MTA Társadalomkutató Központ. 2003. 486. o.
  • MTI Ki Kicsoda 2009, Magyar Távirati Iroda Zrt., Budapest 2008, 440. old., ISSN 1787-288X
  • Adatlap a Magyar Tudományos Akadémia oldalán URL
  • Rövid életrajz a Szegedi Tudományegyetem Mindentudás Egyeteme részén URL
  • Publikációs lista Hatvani személyes egyetemi oldalán URL
  • Hatvani László Wikipédia URL
  • A 20. Szőkefalvi-Nagy Béla Érem az SZTE-professzor, akadémikus Hatvani László matematikusé URL
  • A Körös-toroktól a katedráig: országos elismerés a csongrádi születésű professzornak URL
  • Riportfilm URL
  • Akadémikusok nyakkendő nélkül Hatvani László matematikus 2008. április 17. URL
  1.     Tagadni nehéz!

Az alábbi történet személyes élményem. Pintér Lajossal szigorlatoztattunk Analízisből. Egy hallgatónő rosszul kezdett egy indirekt bizonyítást, mert rosszul tagadta a bizonyítandó állítást. Pintér tanár úr segíteni akart neki, és egy, a mindennapi életből vett példával rá akarta vezetni, hogyan kell az állítást tagadni. Kérte, tagadja a következő állítást: „Minden ember matematikus.” A gyakorlatokon sokszor csinálunk ilyet, és a kolleginának mondania kellett volna a helyes választ: „Van olyan ember, aki nem matematikus.” Felcsillant a szeme, megörült a könnyű kérdésnek, és rávágta: „Nem minden matematikus ember!”

 

  1.     Hogyan kell Rédei professzort jegyzetelni?

A régi időkben az előadásokon nem volt vetítés; az előadó mondta az anyagot, és párhuzamosan a táblára krétával felírta a legfontosabbakat. Bizony, ezt elég nehéz összehangolni. Rédei professzorral is előfordult, hogy a táblára írt szövegbe hiba csúszott. Ha ezt észrevette, akkor azt mondta: „Kedves hallgatóim! Ne azt írják, amit a táblára írok, hanem azt, amit mondok!” Egyszer előfordult, hogy az ismertetett tétel befejezése után rájött, hogy a felírt tétel hibás, de szóban is ugyanolyan hibásan mondta ki. Akkor azt mondta: „Tudják, mit? Az lesz a legjobb, ha nem azt írják le, amit a táblán látnak, nem is azt, amit mondok, hanem amit gondolok!”

 

  1.     Hogyan készítik a négyjegyű függvénytáblázatokat?

Az idősebbek, akik még nem használhattak diákkorukban zsebszámológépeket, mert azok nem is léteztek, emlékeznek a négyjegyű függvénytáblázatokra. Ezeket használtuk a középiskolában például a trigonometrikus számítások elvégzésére. Amikor az előadó az Analízis előadásban a Taylor-polinomokhoz ér, mindig felhívja a figyelmet arra, hogy ezek segítségével lehet kiszámolni a különböző függvények közelítő értékeit, amelyek a függvénytáblázatokban megjelennek. Egyszer az előadásban az érdeklődés felkeltése céljából úgy dramatizáltam a helyzetet, hogy feltettem a költői kérdést: „Mit gondolnak, hogyan készítik a mindenki által jól ismert és használt négyjegyű függvénytáblázatot?” Rögtön meg is akartam válaszolni, ahogyan az a költői kérdéseknél szokás, hogy meghatározzák a Taylor-polinomokat, és azokkal határozzák meg a függvényértékeket. Igen ám, de a kérdés elhangzása után egy hallgató magasba lendítette a kezét, hogy ő tudja a választ. Gondoltam, az még jobb, ha ő mondja el ugyanazt, de meglepetésemre – és a hallgatóság nem kis derültségére –a következő válasz hangzott el: „Vesznek a boltban egy régit és kimásolják belőle.”

  1. Tudhat-e mindent a vizsgázó?

 

A rendszerváltoztatás előtt a legalacsonyabb tudományos fokozat az egyetemi doktori cím volt. Ezt követte a tudományok kandidátusa, majd a tudományok doktora minősítés. Az egyetemi doktori címet az egyetemeken lehetett megszerezni, az utóbbi kettőt a Tudományos Minősítő Bizottság nevű országos szervezetnél. Az egyetemi doktori címért doktori szigorlatot kellett tenni abból a tárgykörből, amelyhez a jelölt disszertációjának témája tartozott. Analízisből mindig Szőkefalvi-Nagy Béla professzor úr vizsgáztatott. Ezeket a szigorlatokat ő fontos intézeti eseménynek tekintette és meginvitálta rá az Analízis tanszék oktatóit. Ő ezt a vizsgát is abban a stílusban vezette, hogy folyamatosan kérdéseket tett fel a szigorlónak. Tudtuk, a professzor úr mindig gondoskodik arról, hogy bármennyire okos is a jelölt, azért ne bízhassa el magát nagyon, ezért a szigorlat mindig úgy ért véget, hogy a legutolsó kérdésnél a vizsgázó „már nem tudott brillírozni”. Persze, ha a jelölt addig jól szerepelt, ettől függetlenül „summa cum laude”-t adott a szigorlatra.

Gehér László, aki a professzor úr tanítványa volt a Bolyai Intézetben, egy kiemelkedően okos matematikus volt. Ez a doktori szigorlatán is bebizonyosodott. Minden kérdésre kiválóan és kimerítően válaszolt. A vizsga már egy órája tartott, amire korábban nem volt példa. A professzor úr megkérdezte a Fredholm-alternatívát, amit közismerten nehéz volt neki úgy elmondani, hogy elégedett legyen vele. Gehér László mindent tudott ebből is. Ekkor a professzor úr megkérdezte: „És mi volt Fredholm keresztneve?” Ezt Gehér László nem tudta. „Érdemes megjegyezni: Ivar Fredholm-nak hívták. Na mindegy, azért rendben volt a felelet. Summa cum laude.” És mindenki megnyugodott, véget ért a szigorlat.

 

A következő független a Bolyai Intézettől; igazából egy, a matematikusok között jól ismert vicc.

 

  1. Lehet-e valamire használni a matematikát?

 

Egy társaság helikopteren utazik. Eltévednek, nem tudják, merre járnak. Megpillantanak a földön egy kis kunyhót, előtte egy ember ül, és úgy tűnik, semmit nem csinál, csak néz maga elé. Lejjebb ereszkednek, és lekiabálnak neki: „Hol vagyunk?” Az ember feláll, „Mindjárt jövök!”, mondja, és bemegy a kunyhóba. Kisvártatva visszajön, és felkiabál: „Helikopteren.” A társaság egyik tagja megállapítja: „Ez az ember biztosan matematikus. Hosszasan elgondolkodott a problémán. A problémára abszolút pontos választ adott. A választ az égvilágon semmire nem lehet használni.”

Kalmár László (1905-1976)

Forrás a képre kattintva látható.

A Bolyai Intézet matematikusaként kezdte, majd a magyar matematikai logika és a számítástudomány egyik alapító atyja lett. Tudományos jelentőségét leginkább az mutatja, hogy az általa alapított intézetet róla nevezték el. (Kalmár László Informatikai Intézet).

 

Született 1905. március 27.-én a Somogy megyei Edde községhez tartozó Alsóbogátpusztán. Apja, Kalmár (Krausz) Zsigmond pápai születésű uradalmi intéző volt, anyja Krausz Róza (1869–1921) kereskedőcsaládból származott. Ötéves kisgyerekként tudása alapján egyből az egytanerős elemi iskola második osztályába vették fel. Nagyon élvezte az osztatlan iskolát: mindig azt figyelte, mit tanulnak a “nagyok”. (A kicsik tananyagát úgyis tudta.) Apja korán meghalt, s a család maradéka Budapestre került. Kalmár ott járt gimnáziumba, s tizenöt éves korában Svájcban is vendégeskedett három hónapot, jótékonysági akció keretében egy gazdálkodó családjában. A jószág őrzése közben itt értette meg egy felsőbb matematikai szakkönyvből Lindemann nevezetes tételének bizonyítását. A tétel azt mondja ki, hogy nincs olyan egész számokkal és alapműveletekkel felírható egyenlet, amelyet megoldva éppen a pi-t (a kör területképletében álló számot) kapnánk. 1922-ben Kalmár pályadíjat nyert az Eötvös-versenyen, majd a budapesti bölcsészkarra járt (akkor a matematika oda tartozott), s diplomája megszerzésének évében, 1927-ben doktorált.

Az egyetem elvégzése után rövid ideig üzemi fizikus volt a Vatea elektroncső gyárban, majd Ortvay Rudolfnak, a Szegedi Tudományegyetem elméleti fizikus professzorának meghívására Szegedre került. 1927-től a szegedi Ferenc József Tudományegyetemre, a Matematikai Intézetben tanársegéd Riesz Frigyes, Haar Alfréd, Kerékjártó Béla mellett. 1932-ben az “Arithmetika és analysis” tárgykörből magántanárrá habilitálták. Riesz Frigyes javaslatára az 1932-33-as tanévben a Matematikai és Természettudományi Kar Kalmár Lászlót bízta meg az Elemi Mennyiségtan Tanszék oktatási, kutatási feladatainak ellátásával, a tanszék azonban elhalt, mert a minisztérium takarékossági okokból nem nevezett ki professzort. Tudományos munkája elismeréseként 1936-ban König Gyula díjjal jutalmazták.

Minden érdekelte, ami matematika, de nem csak az: a Szegedi Fiatalok Művészeti Kollégiuma is, olyannyira, hogy az e legendás intézmény belső köréhez tartozó Árvay Erzsébet tanárjelölt tanítványát vette feleségül.

Egészen különleges dolgokba is belevágott. Az Acta megindulása után Szegeden felnőtt egy nyomdai szakembergárda is – ennek első generációját Radó Tibor és Kalmár László képezte ki a matematikai jelek helyes szedésére – akik azután évtizedeken keresztül a hazánkban kiadott matematikai és fizikai tárgyú könyvek tekintélyes részének szedését végezték. 

A Kőnig Gyula érmet már 1936-ban elnyerte. Professzori kinevezésére mégis 1947-ig kellett várnia, adjunktusként (docensi státus akkoriban nem létezett).

1940. október 19-én a Ferenc József Tudományegyetem visszaköltözött Kolozsvárra, helyében azonnal megalapították Szegeden a Horthy Miklós Tudományegyetemet. Megkezdődtek az átigazolások, Kalmár László magántanári habilitációját nem ismerték el ezen az egyetemen a faji üldöztetés miatt. 1944 tavaszán a Sztójay-kormány fajüldöző rendelete nyomán adjunktusi állása és szakóraadói tevékenysége alól is felmentették. Szegedi építkezéseken dolgozott munkaszolgálatosként – innen is matematikai témájú levelezéseket folytatott. Nagy nehezen megúszta a deportálást (állítólag megszökött), s Szegeden már 1944 októberében eltörölték a fajüldöző törvényt az egyetemen, visszavették Kalmár Lászlót adjunktusnak, s egyike volt azoknak, akik a matematika oktatást és kutatást feltámasztották a háborús károk által sújtott egyetemen.

1945 áprilisában elismerték Kalmár László magántanári habilitációját. Riesz Frigyest meghívták és kinevezték a budapesti egyetem III. sz. Matematika Tanszékére, utódja Szegeden 1947. március 18-án Kalmár László lett, mint a felsőbb mennyiségtan nyilvános rendes tanára, s mint a Bolyai Intézet igazgatója. A második világháborút követő években Rédei László munkatársa, majd Kalmár László tanársegédje volt Szele Tibor, az absztrakt algebra híres művelője. 

A Magyar Tudományos Akadémia 1949-ben választotta levelező, 1961-ben rendes tagjai sorába. 1952-ben érte el a nagydoktori fokozatot. 1949/50-ben ő látta el a szegedi egyetem rektori teendőit. A továbbiakban számos tudományos tisztséget töltött be, s működött szakmai társaságokban, szerkesztett lapokat. (A hagyomány szerint volt olyan időszak, amikor egyszerre 50 tisztségben, szervezetben, szerkesztőségben, bizottságban vett rész.)

Ötven éves volt, amikor “pályát módosított”. A negyvenes évek folyamán a matematikai logika képletei mellé Neumann János és munkatársai műhelyéből kikerültek az első működő számítógépek. Hazánkban Kalmár volt az a tudós, aki képes volt felfogni a számítógéptudományt. Kalmár László élete utolsó két évtizedét a hazai számítástudomány és számítástechnika felvirágoztatására fordította. Ennek Szegeden már az ötvenes évek végén megszületett az első eredménye. Ez az M3 volt, a hatalmas termet betöltő szörnyeteg, temérdek “rádiólámpájával” (Szüleim és kortársaik még így nevezték az elektroncsöveket – hosszú percekig tartott, mire bekapcsolás után működőképessé melegedtek…) A számítógépekben ezeket hamarosan felváltották a tranzisztorok, majd a chipek), körülbelül akkora teljesítménnyel, mint az 1980-as évek slágere, a jó emlékű Commodore 64.

A számítástudománnyal együtt indult a vezérléstudomány, mára már-már elfeledett nevén a kibernetika, amely azt próbálta megragadni, mi a közös a számítógépek, az élőlények és a társadalmak működésében. Az akkori hivatalos filozófusok hamar rá is ragasztották a “burzsoá áltudomány” címkét, mondván, hogy nem is lehet közös bennük, hiszen különböző mozgásformákban működnek (!?), másrészt pedig mind­egyiknek úgyis megvan a maga egyedül üdvözítő elmélete. A Szovjetunió szakemberei nem hagyták magukat: kibernetika helyett “automatika és távmechanikát” mondtak, és csinálták tovább a kibernetikát. Kalmár Szegeden még csak át sem keresztelte: szemináriumot indított belőle, aztán Muszka Dániellel együtt megcsinálta a kibernetikus „katicabogarat”, meg a logikai gépet, amelyeket “szegedi” jelzővel tart számon a tudománytörténet. Hazahozta a legnagyobb nyugati kutatók friss, azóta klasszikussá vált cikkgyűjteményét, az Automata Studies-t. Ez a könyv és Kalmár ezidőtájt írt cikkei indították el a mindmáig nemzetközi tekintélyű szegedi automataelméleti iskolát. Folyóiratot is alapított: a több mint harminc éves, mindmáig szegedi illetőségű Acta Cybernetica – a magyar számítástudományi folyóirat – első főszerkesztője volt.

1956-ban a szegedi Bolyai Intézet keretében alakult meg az MTA Matematikai Kutató Intézetének Funkcionálanalízis Osztálya Szőkefalvi-Nagy Béla vezetésével, 1957-től pedig az MTA Matematikai Kutatóintézetének Matematikai Logika és Alkalmazásai csoportja (1958-tól Osztálya) Kalmár László vezetésével. E két kutatási egység 1967. január 1-jétől az MTA Analízis Tanszéki Kutatócsoportjává, illetve az MTA Matematikai Logikai és Automataelméleti Kutatócsoportjává alakult át.

1971-ben a Matematikai és Számítástudományi Tanszék kettévált, a Halmazelméleti és Matematikai Logikai Tanszék vezetője Fodor Géza lett, a továbbiakban Kalmár László a Számítástudományi Tanszéket vezette egészen 1975. októberi nyugdíjazásáig.

Örökmozgó, állandóan szervező, a matematikát, a tanítást, az életet szenvedélyesen szerető ember volt. 1976-ban, Mátraházán, nyaralás közben érte a halál, a szegedi Belvárosi temetőben nyugszik.

Első oktatói éveiben néhány függvénytani és számelméleti eredménye mellett úttörő dolgozatot tett közzé a játékelméletről (mai terminológia szerint a kombinatorikai játékok elméletéről), továbbá, mint Edmund Landau megjegyzi az analízis alapjairól írt klasszikus könyvecskéjének előszavában, kijavította a természetes számok axiomatikus felépítésének egy rejtett fogyatékosságát. Alkotó erejét két olyan területen fejtette ki igazán, amelyeknek még a létjogosultságáért is meg kellett küzdenie. Ezek egyike a matematikai logika, a másik pedig a hozzá – mint később kiderült – szorosan kapcsolódó, de a harmincas években, a matematikai logika egyik fénykorában még nem is létező számítástudomány volt. Amikor első matematikai logikai közleménye megjelent, még maga Riesz sem tekintette a matematika részének ezt a tudományágat, mint ahogy negyedszázaddal később sem vívta ki kollégái lelkesedését, amikor első számítástudományi dolgozatát publikálta. A matematikai logika akkor újdonságnak számító, azóta közkinccsé vált nagy eredményeire Kalmár egyszerűbb bizonyítást adott, s mindenki másnál élesebben ismerte fel összefüggéseiket. Ennek az éleslátásnak köszönhetően, amikor a rekurzív függvények és az algoritmusok szakértőjeként találkozott a számítógépi programokkal, a számítástudomány elkötelezett hívévé és művelőjévé vált.

A 20. század utolsó évtizedeiben bekövetkező információrobbanás egyik előfutára és előkészítője volt a matematikai logika és a számítástudomány területén. E területeken kifejtett elméleteinek (játékelmélet, algoritmusok) még a létjogosultságáért is meg kellett küzdenie. 1962-ben életre hívhatta a Kibernetikai Laboratóriumot, amelyben 1964-ben már számítógép működött. Ez a Laboratórium és Kalmár László Számítástudományi Tanszéke képezte alapját a mai Informatikai Tanszékcsoportnak a szegedi egyetemen, ahol programtervező és programozó matematikusok képzése folyik. Kalmár László idejében alkalmazott matematikusok képzéséről beszéltek, de ezt tette Kalmár László már 1957-től kezdve, nála meg lehetett ismerkedni a kibernetika legújabb eredményeivel. A világ legnagobb számítógéptudományi társasága, az IEEE Computer Society méltán tartja őt számon a számítástudomány nagy úttörõi között.

Tudományos közleményeit német, francia és angol nyelven adta közre.

  • MTA Matematikai Bizottság (1953–1976)
  • Filozófiai Főbizottság (1957–1976)
  • Tudományfilozófiai Nemzeti Bizottság, tag (1958–1976)
  • Elnökségi Kibernetikai Bizottság, tag és elnök (1961–1970)
  • TMB Matematikai Szakbizottság (1963–1976)
  • Nyelv- és Irodalomtudományi Osztály Matematikai és Alkalmazott Nyelvészeti Munkabizottság (1964–1976)
  • Matematikai Kutató Intézet Tudományos Tanácsa (1965–1976)
  • Számítástechnikai Központ Tudományos Tanácsa tagja, (1965–1976)
  • SZAB Matematikai, Fizikai és Kémiai Szakcsop. és Szakbiz. tag
  • Kibernetikai és Számítástechnikai Munkabizottság elnöke (1969–1976)
  • Association for Symbolic Logic Comm. Logic in Europe tagja (1966–1976)
  • Int. Federation for Inf. Processing Working Group 2.2 tagja (1967–1976)
  • OMFB tagja (1970–1976)
  • Acta Cybernetica főszerk. (1969–1976)
  • Acta Mathematica Hungarica (1956–1976)
  • Matematikai Lapok (1950–1976)
  • Studia Sci. Math. Hung. (1966–1976)
  • Információ – Elektronika (1966–1976)
  • Periodica Math. Hung. (1970–1976)
  • Journal of Symbolic Logic (USA, 1944–1951)
  • Zeitschrift für Math. Logik und der Math. (NDK, 1955–1976)
  • Archív für Math. Logik und Grundlagenforschung (NSZK, 1956–1976)
  • Elektronische Inf. und Kybernetik (NDK, 1965–1976)
  • Természettudományi Társaság (1926–1976)
  • Eötvös Loránd Matematikai és Fizikai Társaság (1926–1976)
  • Bolyai János Matematikai Társulat (1947–1976)
  • Neumann János Számítógéptudományi Társaság, tiszteletbeli elnök (1969–1976)
  • Magyar Nyelvtudományi Társaság (1962–1976)
  • Magyar Pedagógiai Társaság (1969–1976)
  • Gesellschaft Angewandte Mathematik und Mechanik (1960–1976)
  • König Gyula jutalom (1936)
  • Kossuth-díj ezüst fokozat (1950)
  • Beke Manó emlékdíj (1958)
  • Felszabadulási jubileumi emlékére (1970)
  • Szele Tibor-emlékérem (1970)
  • Állami Díj első fokozat (1975) – A matematika alapjainak kutatásában és a számítógépek elméletében elért eredményeiért.
  • József Attila emlékérem (1975)
  • Neumann János emlékérem (1976)
  • Magyar Örökség díj (2002) /posztumusz/

Rédei László, Kalmár László és Szőkefalvi-Nagy Béla emléktáblája a szegedi Pantheon falán (Kalmár Márton alkotása)

A szegedi egyetemen a Kibernetikai Laboratórium, mára már az Informatikai Intézet nevet viseli, s mindenekelőtt Kalmár László nevét: Kalmár László Informatikai Intézet, valamennyi hallgató és egyetemi dolgozó mind a mai napig ott tanulja az informatika alapjait.

  • A Bolyai Intézet története URL
  • A szegedi egyetemi matematikai intézetek hetvenöt éve URL
  • Varga Antal: Kalmár László, a magyarországi számítástudomány atyja. Polygon (matematikai, szakdidaktikai közlemények), Szeged, VII./1.; 1997 június
  • Varga Antal: Kalmár László, az ember. Polygon (matematikai, szakdidaktikai közlemények), Szeged, XI./2.; 2002 június
  • Csákány Béla: Kalmár László : (1905-1976). Szegedi műhely, 44.2005:2, 115-121. p.
  • Szegedi egyetemi almanach : 1921-1970. Szeged, Márta Ferenc – Tóth Károly, 1971. Kalmár László lásd 171-172. p.
  • Szegedi egyetemi almanach : 1921-1995. I. köt. (1996). Szeged, Mészáros Rezső. Kalmár László lásd 328-329. p Szegedi egyetemi almanach : 1921-1970. Szeged, Márta Ferenc – Tóth Károly, 1971. Kalmár László lásd 171-172. p.
  • Csákány Béla – Varga Antal: Matematika. In A Szegedi Tudományegyetem múltja és jelene: 1921-1998 = Past and present of Szeged University. /JATE. Szeged : Officina Ny., 1999. 380-402. p.
  • Varga Antal: Kalmár László, a magyarországi számítástudomány atyja. Polygon (matematikai, szakdidaktikai közlemények), Szeged, VII./1.; 1997 június
  • Varga Antal: Kalmár László, az ember. Polygon (matematikai, szakdidaktikai közlemények), Szeged, XI./2.; 2002 június
  • Csákány Béla: Kalmár László : (1905-1976). Szegedi műhely, 44.2005:2, 115-121. p.
  • Kalmár László: Gyertek, bizonyítsuk be Csebisev tételét!, 1., 2., 3., Középiskolai Matematikai Lapok
  • Csákány Béla: A második triumvirátus (Rédei László, Kalmár László, Szőkefalvi-Nagy Béla) URL
  • Szent-Györgyi lovon? Válogatás a Szegedi Tudományegyetem Természettudományi és Informatikai Karának anekdotakincséből / szerk. Szabó Péter Gábor.. Szeged, Szegedi Tudományegyetem TTIK, 2014.
  • Csirik János: A szegedi iskoláról URL
  • Kalmár László munkássága URL
  • Kalmár-féle logikai gép URL
  • Kalmár László Wikipédia URL
  • Kalmár László: Gyertek, bizonyítsuk be Csebisev tételét!, 1., 2., 3., Középiskolai Matematikai Lapok

Anekdoták Kalmár Lászlóról 

 

1974-ben Saarbrückenben voltunk az egyik legrangosabb konferencián, az ICALP ’74-en. A szakma egyik vezető szakembere tartotta az előadását, mi az első sorban ültünk, Laci bácsi írta szokásos képeslapjait. Az előadás végén jöttek a kérdések, hozzászólások. Úgy nézett ki, hogy már vége a vitának, amikor Laci bácsi felnyújtotta a karját: nem értem, hogy a táblán lévő számítógépes program 23. sora után hogyan jön a 24. Mire az előadó a belső zsebéből kivesz egy cetlit, hol a papírra, hol a táblára néz, majd megszólal: elnézést kérek, a másolásnál kimaradt öt sor.

Az alábbi anekdoták a következő könyvből származnak:

Szent-Györgyi lovon? Válogatás a Szegedi Tudományegyetem Természettudományi és Informatikai Karának anekdotakincséből / szerk. Szabó Péter Gábor.. Szeged, Szegedi Tudományegyetem TTIK, 2014.

 

MATEMATIKAI LOGIKA

1930 körül a Bolyai Intézet nagyjai kevéssé ismerték és kevésre becsülték a matematikai logikát, aminek aztán az akkor ifjú Kalmár László lett a mestere. Ezt mutatja Haar Alfréd emlékezetes kérdése Kalmár magántanári habilitációja előtt: – És mondja, Kalmár doktor, a matematikai logikában is vannak definíciók, tételek és bizonyítások? Vagy csak úgy beszélnek a témáról, mint a filozófusok? (Csákány Béla jegyezte le)

 

MIVEL EGYENLŐ AZ IKSZ?

Kalmár László – enyhén szólva – szangvinikus vizsgáztató volt. Abszolút marhaságot hallván a diák szájából, olykor kétségbeesett haragra gerjedt. Egy alkalommal az inverz függvényről szerette volna faggatni a delikvenst, és bevezetésül megkérdezte:- Szinusz iksz egyenlő ával, mivel egyenlő iksz?A vizsgázó megörült a könnyű kérdésnek és diadalmas arccal kivágta:- Iksz egyenlő á per szinusz!(Ilyen esetekben rohant ki Kalmár a táblához, hogy az ott ijedten toporgó diákot észre térítse – többnyire kevés sikerrel.)

(Csákány Béla jegyezte le)

Kalmár László volt talán a legélesebb eszű ember, akivel a jósorom összehozott. Máig emlékszem, hogy másodév legvégén már nem akart új anyagot előadni és – merészen – azt mondta a mat-fiz, fiz-mat évfolyamnak, hogy kérdezzünk valamit és arról még beszél. Már nem emlékszem, melyikünktől származott a fizikát matematikailag pongyolának tartó évfolyam kérdése, de a következőt kérdeztük: „Az egyesített gáztörvényben az (1+at) faktor miért nem a négyzeten szerepel, hiszen ha a V=VO(l+cct)-t és a p=pO (l+at)-t összeszorozzuk, a m i szabályos eljárás egyenletek esetén, a faktornak a négyzeten kellene szerepelnie. Laci bácsi habozás nélkül elmondta a függvények értékkészletének és értelmezési tartományának kérdését és megmagyarázta, hogy miért hibás az összeszorzás. Ez után a személyes történet után egyáltalán nem lepett meg, hogy amikor komputert akart építeni, egy pár hónapos villamosságtan tanulás után – amint évfolyamtársam, Muszka Dániel mesélte nekem annakidején – kapcsolási rajz mélységű tervet adott át neki megépítésre…(Gyulai József lejegyzése)

A Nagy trió, 

Kalmár-Rédei-Szőkefalvi mindannyiunkban mély nyomokat hagyott. Annak az „ádáz barátságnak” egy eseménye, ami Kalmár László és Szőkefalvi-Nagy Béla között zajlott, a fülem hallatára történt. Közismert volt, hogy Rédei jegyzete a leglakonikusabb. Szőkefalvié volt a kifogástalan méretű, pont az intelligens diák­hoz méretezett. Kalmáré meg a másik véglet… Egy alkalommal, Szőkefalvi óráján rákérdezett egy, az analízis tárgyba tartozó tételre. A felszólított évfolyamtársam nem tudta a választ, mire „Szőke”: „Hogy-hogy nem tudja, hiszen Kalmár professzor jegyzetének a háromezer-kétszáz-negyvenedik oldalán megtalálható.”(Gyulai József lejegyzése)

KALMÁR-ELŐADÁSON

Kalmár Laci bácsi a hetvenes évek elején tartott nekünk Gépi programozást. Úgy emlékszem, hogy mindig elegánsan érkezett: öltöny, nyakkendő, egyik kezében a táskája, másik karján a frissen vasalt barna köpenye. – Kedves hallgatóságom – kezdte az előadását és az átöltözést. Miközben folyamatosan, érdekfeszítően és hi­bátlanul tartotta az előadását, levette a zakóját, a szék háttámlájára tette, majd a nyakkendője következett, felvette a köpenyét, minden gombját begombolta, majd a nyakkendőjét bal kézfejére feltekerte és a zakó zsebébe tette. Ha előadás közben melege volt, akkor köpeny le, az öltöny mellénye le, majd köpeny fel és mindezt folyamatos beszéd és séta közben. Gyakran használta a táblát, ezt az előadás végén mind a köpenyén, mind a kezén látni lehetett. Ha pedig éppen nem írt fel valamit a táblára, akkor sétált az ablakig, majd vissza katedra előtt az ajtóig és a tábla előtt folytatta az ablakig, körbe-körbe. Történt egyszer, hogy séta közben az ajtó mellett lévő fogason egy olyan télikabátot fedezett fel, amelyiken volt egy kis pihe. Ezt nem tűrhette, krétás kezével egy mozdulattal eltávolította, majd folytatta a sétáját az ablak felé. Mikor ismét a kabátnál járt, felfedezte a pihe helyén éktelenkedő kréta­foltot, amit a másik, még krétásabb kezével egy laza mozdulattal letörölt onnan. Ahogy rótta a köröket és minden körben javítani igyekezett előző körben elkövetett hibáján, a folt egyre nagyobb és egyre fehérebb lett. Az előadás végén fehér ujjú sötét télikabátot vett le a fogasról Orbán Gabi évfolyamtársunk és a teljes szünet se volt elég, hogy leporoljuk. (Dévényi Károly)

VÖRÖSBOR TISZTÁN

Egy másik alkalommal Laci bácsi jókedvűen érkezett. Nagy lendülettel kezdte meg előadását az elmaradhatatlan átöltözős jelenettel kísérve. Egyszer csak ész­revette, hogy az asztalra tett aktatáskájából valami folyik. Valami vörös. Ki az asztalra, majd onnan a földre. Egy pillanatra se szakította meg mondanivalóját és közben elkezdte a táskáját kipakolni. Szomorúan vette észre, hogy egy boros­üveg repedt meg és a vörösbor mindent eláztatott, többek között fontos, hivatalos levelezést is, amit az Akadémiával és a Minisztériummal folytatott. Az iratokat tehát nem lehetett kidobni, meg kellett szárítani. Sorban vette elő a táskájából, kicsit megtörölte, majd az előadóterem első sorában kiterítette száradni. Sok irat volt a táskájában, következett a második sor és így tovább. Ha akkor készült volna hangfelvétel, talán csak a papír zizegése zavarta volna az előadást, de a történtek nem, Laci bácsi rendületlenül mondta. Mint a végén kiderült, az akkor még a Bolyai épület földszintjén működő Egyetemi Számítóközpont munkatársai köszöntötték fel születésnapja alkalmából főnöküket, aki ennek nagyon örült és az előadására lendületesen igyekezve valamelyik ajtófélfának csapta a táskáját. Az előadás végére az előadóteremben erős kocsmaszag volt. Akik szerettek az első sorok valamelyikében ülni, most elnyerték méltó jutalmukat, majd hogy nem inhalálták a vörösbort. Egyik hallgatótársunk meg is jegyezte kifelé menet:- Azért egy kis szódát igazán felszolgálhattak volna. (Dévényi Károly)

A VEKKER

Kalmár professzor híres volt arról, hogy szerette lényegesen tovább tartani az előadást, mint ahogy az órarend szerint tehette volna. Egyszer figyelmeztették, hogy ezt a hallgatóság nehezményezi. A következő előadásra magával hozott egy vekkerórát, felhúzta és az asztalra tette. Amint megszólalt a vekker, szünetet tartott, szünet után a megkezdett mondat másik felével folytatta az előadást. (Máté Eörs)

GENERÁCIÓVÁLTÁS

Amikor az egyetem megkapta az Akadémiai Székházat, akkor gondoltak arra, hogy valamikor oda is kerülni fog egy számítógép, és kialakítottak egy termet, az ajtajára kiírták: SZÁMÍTÓGÉP TEREM. Amikor megérkezett a MINSZK-22, akkor le kellett szerelni az M3-at, hogy legyen helye az új gépnek. A leszerelt gépet átszállították az Akadémiai Székház számítógép termébe. Néhány nap múlva valaki tréfás kedvében a felirat egy betűjét kicserélte, így lett a felirat: SZÁMÍTÓGÉP TETEM. (Máté Eörs)

KALMÁR VIZSGÁZTAT

Kalmár László szeretett a Riesz teremben vizsgáztatni, mert a hátsó ajtón a közönség anélkül jöhetett-mehetett, hogy zavarta volna a vizsgát. Kalmár szerette a közönséget is, és a közönség is ezeket a vizsgákat, mert gyakran érdekes jeleneteknek lehettek tanúi. Egyik alkalommal a vizsgázónak a függvények folytonosságáról kellett volna beszélnie, de Kalmár sehogy sem tudta rávenni a hallgatót, hogy elmondja a definíciót. Végül Kalmár azt mondta:- írja le, írja le, hogy mit jelent az, hogy egy f(x) függvény az xO pontban folytonos! Hogy a hallgató időt kapjon, Kalmár körbe sétált a teremben, néhány szót váltott az emberekkel, a hölgyeknek kezet csókolt,…Amikor végzett a sétával, megnézte, mit írt a hallgató.- Már elkezdte! – mondta boldogan – Hogy egy f(x) függvény az xO pontban folytonos az azt jelenti, hogy…Tett még egy kört, az előzőhöz hasonlóan, majd mikor látta, hogy a hallgató nem írt többet, szó nélkül beírta az elégtelent. (Máté Eörs)

Gévay Gábor mesélt egy másik “Kalmár vizsgáztat” történetet:

Egy hallgató nagyon nem tudott. Kalmár professzor egyre idegesebben hallgatta, aztán nem bírta tovább, félbeszakította: “Ne mondjon ilyet, mert kiugrom az ablakon!” A hallgató próbálkozott tovább. Kalmár prof. odalépett, és látványosan kitárta az ablakot. Pár további elhangzott mondat után kiabálva félbeszakította a vizsgázót: “Gyilkos! Gyilkos!”.

KALMÁR LACI BÁCSI

Szívesen tanult és járt konferenciákra. Általában az első sorok valamelyikében ült, s szorgalmasan jegyzetelt. De nem sokáig maradt csöndben, hamarosan kérdéseket tett fel, vagy megjegyzéseket tett. Mondják, egy Moszkvában tartott nemzetközi konferencián egy új elméletet mutatott be egy professzor társa. Laci bácsi késve érkezett, ismerőseinek barátságosan integetve leült valahol elől. Szorgalmasan jegyzetelt vagy öt percig, majd megértve azt, hogy mire megy ki a dolog, kirohant a táblához, s azt mondta: kolléga, ez így túl körülményes, és felvázolt egy új, elegáns megoldást. Egyetlen nagy ellenfele volt, az idő. Mondják, a Stockholmi világkongresszuson, ahol 15, maximum 20 perces előadások voltak, ismerve és elismerve őt, néki 30 percet adtak, a szünet előtt. Többszöri idő figyelmeztetés ellenére sem tudta befejezni az előadást, s azt folytatta a szünet alatt is. Emlékszem, 1968-ban Esztergomban egy automatikus programozási nyelvek szemináriumon, az ALGOL-68-at tanultuk együtt a nyelv szerzőinek egyikétől, Wijngaarden professzortól. Noha Laci Bácsinak is új volt az anyag, tüstént gyakorlatvezetést vállalt. Óriási méretű (nem lehúzható) táblák voltak, s miután az elérhető felületet teleírta, széket hozott, arra felállva, fent folytatta. Majd amikor ott is elfogyott a hely, hátraszólt az egyik nyelvész kollégának: Dénes tedd arrébb a székemet! Majd madárfogással felfüggeszkedve a tábla tetejére, arrébb araszolt, ez a tekintélyes, korpulens ember. Szívélyes, mosolygós ember volt, de hamar dühbe gurult, például ostoba diákok vizsgáztatása közben, s ilyenkor repültek a kréták, verte a táblát, s hatalmas erejű hangon nyilvánított nemtetszést. Otthon kínai zenét hallgatott szívesen – csendben. (Havass Miklós)

MEGHALT SZTÁLIN

Az ötvenes évek elején Szőkefalvi-Nagy Béla előadást tart a Riesz teremben. Nyílik az ajtó, Kalmár Laci bácsi áll ott, és megrendülten annyit mond:— Meghalt Sztálin. Rövid szünet után Szőkefalvi:- Folytathatom az előadásomat professzor úr? (Csendes Tibor)

KARCAGRA MENET

Kalmár László, tudós hivatásának megfelelően, állandóan utazott a világ minden sarkába. Ha nem oda, akkor csak Pestre, igen sűrűn, szinte hetente. Szinte mindig úton volt. Ámde, történetünk idején először utazott a nászasszonyukhoz Karcagra, s még nem ismerte az utat. Feleségével Erzsikével Cegléden szálltak át a debreceni vonatra, ahol már egy fél óra után Kalmár nyugtalankodni kezdett:- Csömpe! – így szólította feleségét – Vedd le a csomagokat!- Lacikám, – volt a szelíd válasz – ráérünk, messze van még a leszállás. Öt-tíz perc múlva újra megszólalt:- Csömpe, mi lesz már? Itt maradnak a csomagok! S miután ez a párbeszéd többször megismétlődött a következő órában, rászólt Erzsikére a kupéban szemben ülő fejkendős nénike:- Ugyan már kedves, vegye már le neki azokat a csomagokat! Látszik, hogy a bácsi nincs hozzászokva az utazásokhoz, azért ilyen nyugtalan! (S. Radimetzky Györgyi)

DÍSZÍTŐ JELZŐK

Pollák György számos szellemes, de csípős „díszítő jelzőt” talált ki kollégái szá­mára, saját szavai szerint olyanokat, amelyeknek az érintett örülne ugyan, de esetleg csak titokban. Tiszteletben tartva a leszármazottak esetleges érthető érzékenységét, itt csak három szelíd díszítő jelzőt idézünk föl: Durszt Endre, a felsőoktatás hatalmas gépezetének szerény, de megbízható csavarja. Kalmár László, az aktivitás lojális mártírja. Stachó Lajos, az érvényesülésért küzdő sokoldalú tehetség. Kalmár díszítő jelzőjének magyarázata: ő temérdek feladatot és megbízatást vállalt, tisztségeinek száma fénykorában elérte az ötvenet [!]. Heppes Aladár budapesti matematikustól ered a következő álközmondás: „Nincsen ankét Kalmár nélkül.” (Csákány Béla)

 

A következő történethez tudni kell, hogy a japán nyelvben nincs „1” hang, az „r” pedig nem ropogós, inkább 1-szerű. A hetvenes évek elején Kalmár László professzorhoz néhány napos látogatásra japán tudós érkezett, s a szegedi akadémiai épületben szállt meg. Lön vasárnap reggel, mégpedig parlamenti képviselőkre való szavazás napja, és Kalmár szokása szerint benézett az akadémiai házba, ám szokásától eltérően elegáns öltözetben. Látva a japán kolléga meglepett arcát, az utóbbit meg is magyarázta:- Today I have election. Majd a fokozódó érdeklődés láttán így folytatta:- This happens once in four years. How often do you have elections at home, in Japan? A vendég, hangjában alig leplezett büszkeséggel, készségesen válaszolt:- Oh, every night, every night! (Csákány Béla)

MINDENKI MÁSKÉPP CSINÁLJA

Talán Pollák Györgytől származik az az összeállítás, hogy melyik professzor hogy megy WC-re.

Szőkefalvi-Nagy Béla: Óvatosan körülnéz, nem látja-e valaki.

Kalmár László: Előtte kikéri az állami és pártvezetés véleményét.

Tandori Károly: Elnézést kér mindenkitől, ha ezzel zavarna valakit.

Rédei László: Tessék, Klárika, intézze el! (Máté Eörs)

 

ÖNFÉNYKÉPEZÉSI LAP

Egy nap — 1951. május 7.

Kalmár László (1905-1976) matematikaprofesszor, amikor a szegedi egyetem rektora volt, feljegyezte egy napjának pontos eseményeit. Talán egyetlen más híres matematikusnak sem ismerjük egy napját ilyen pontosan. Éppen 70 évvel ezelőtt történt.

0h—0h45’ jegyzetírás az intézetben mert otthon rövidzárlat volt (Anal. II, 148-150. oldal)

0h45’—0h55’ kapunál várás, hazajövés

1h20’— vacsora melegítés, vacsora, lefekvés elálmosodásig (kb. 1/2 óra) Rasiowa-Sikorski, A proof of the completeness theorem of Gödel, Fund. Math. 37 (1950), 193-200 olvasása

elalvástól 7h alvás

7h—8h20’ borotválkozás, mosdás, öltözködés, reggelizés, közben (tanulmányi osztály, rektori hivatal)

8h20’—8h30’ intézetbe bemenés

8h30’—11h02’ diktálás (Grebencha-Novoselov: Matematikai Analízis I. bírálata; mellékelve). Közben 11h21’-kor Károlyi elvtárs pályamunkát hoz, két perccel később két körözvényt.

11h02’—11h20’ a lediktált bírálat átnézése, képletek beírása, közben Dux elvtárs 11h06’-kor megkérdezte, hogy a térbeli Laplace-egyenletnek 1/r^2-e a megoldása vagy 1/r.

11h20’—11h40’ az ábrák és a bírálat átadása Kemenes Elvtársnak párt; Anal. II. jegyzet állásának ellenőrzése Bereczkinél és Róthnál. 

11h40’—11h45’ átmenés rektori hivatalba, közben lépcsőn Gergely elvtársnővel az intézeti beteglátogatási teendők megbeszélése 

11h45’—13h15’ folyó ügyek rektori hivatalban 

13h15’—13h20’ hazajövetel

13h20’—13h25’ otthoni posta átnézése (akadémiai levelezés)

13h25’—13h55’ Anal. II. jegyzetírás 

13h55’—14h20’ ebéd 

14h20’—15h pihenés

15h—21h Anal. II. jegyzetírás, közben Dombóvári elvtárs táviratot hoz (VKM, Grebencha ábrák sürgetése)

21h—24h Anal. II. jegyzetírás (170 oldalig)

Itt ha az utolsó sorban az alvásra fordított heti 28 órát napra szeretnénk lebontani és a 28-at 7-tel elosztjuk, azt kapjuk, hogy az átlagosan napi 4 órát jelent, ami nem valami sok…Szabó Péter Gábor

 

(Lejegyezte Gécseg Ferenc) URL

Kérchy László (1951-)

Forrás a képre kattintva látható.

Matematikus. 1951. nov. 14.-én született Baján. Általános iskolában Jäger Antal, a III. Béla Gimnáziumban Hegedűs József tanár urakra emlékezik nagy szeretettel, mint akik segítették kibontakoztatni matematikai érdeklődését. A Középiskolai Matematikai Lapok rendszeres feladatmegoldója volt. Baján érettségizett, majd a szegedi egyetemre jelentkezett. A JATE-n szerzett kitüntetéses programtervező matematikus diplomát 1975-ben, azóta a JATE illetve a SZTE Bolyai Intézetében dolgozik.1979-ben summa cum laude egyetemi doktor, 1982-ben a matematikai tudományok kandidátusa, 1989-től doktora. 

Disszertációi: egyetemi doktori: P-gyenge kontrakciók – témavezetője Szőkefalvi-Nagy Béla. Kandidátusi disszertációja: Kontrakciók bizonyos osztályairól. Tudományok doktora disszertációjának címe: Hilbert térbeli kontrakciók vizsgálata izometrikus aszimptotákkal.

1975-től tanít a JATE (majd 2000-től az SZTE) Analízis Tanszékén, 1975-től 1979-ig tanársegéd,  1980-1984 között adjunktus, 1985-1989 között docens, 1990-től egyetemi tanár.

Több ízben vendégprofesszor az Indiana University, majd a University of Tennesse és a Texas A & M University meghívására.

A JATE Eötvös Loránd Kollégiuma Igazgató Tanácsának elnöke 1990-1997 között. 2005-től 2011-ig az SZTE Matematikai Tanszékcsoportjának (Bolyai Intézet) tanszékcsoport-vezetője. 2005 és 2015 között a SZTE Analízis Tanszék vezetője. Számos tudományos bizottság tagja (JATE-SZTE Doktori Tanács, MTA Matematika Bizottságának tagja, majd alelnöke, a SZTE Szenátusának tagja).

1980-tól a Bolyai János Matematikai Társulat, 1995-től 2011-ig az American Mathematical Society tagja.

1986-tól az Acta Scientiarum Matematicarum című folyóirat szerkesztője majd főszerkesztője (1993-2017). 

Eddig 76 nemzetközi konferencián, kongresszuson vett részt, illetve tartott előadást.

Kitüntetései: Alexits György-díj (1990), Bolyai Farkas-díj (2002), Akadémiai Díj (2005), Magyar Felsőoktatásért Emlékplakett (2005), Charles Simonyi kutatói ösztöndíj (2005), Pro Universitate díj (2012), Szőkefalvi-Nagy Béla érem (2012), Magyar Érdemrend Tisztikeresztje (2013), Klebelsberg Kunó díj (2016).

Felesége egykori évfolyamtársa, Kovács Éva. Lányai: Anna (SZTE, BTK, Angol-Amerikai Intézet) és Vera (Összehasonlító Irodalomtudományi Tanszék). Öt unoka büszke nagyapja: Sára (18), Lilla (16), Alma (14), Miklós (9) és Vilmos (6).

Szabadidős kedvtelései: a zene (gyermekkorától kezdve), az irodalom (kedvenc ifjúkori olvasmánya Thomas Mann: József és testvérei című regénye), a horgászat és a kertészkedés.

Kérchy László: Valós- és funkcionálanalízis URL

Hilbert terek operátorai URL

Harmonic Analysis of Operators on Hilbert Space URL

 

Fontos visszajelzések : Beszélgetés Kérchy Lászlóval. A riportot készítette Pintér M. Lajos (Szegedi Egyetem 53. évf. 2005 .28. szám) URL

Saját kutatási területéről a következőket írta:

“A Hilbert tér nevét a XIX. század végének és a XX. század elejének egyik legnagyobb hatású matematikusáról, a német David Hilbertről kapta. Ezen végtelen dimenziós terek tanulmányozásához fizikai jelenségeket leíró integrálegyenletek vizsgálata vezetett. Az elmélet fejlődésének hatalmas lökést adott az atomi rendszerek fizikájának, a kvantummechanikának a kidolgozása az 1920-as években. Kiderült ugyanis, hogy a Hilbert terek operátorai (folytonos, lineáris transzformációi) kiválóan alkalmasak a kvantummechanika törvényeinek matematikai leírására. A Hilbert tér axiómarendszerét a fiatal Neumann János adta meg, aki egyúttal a kvantummechanika matematikai alapjait is lefektette. A modern számítógép működési elvének kigondolójaként számon tartott világhírű hazánkfia az operátorokkal kapcsolatos eredményeit tudományos pályafutása legnagyobb teljesítményei közé sorolta. A funkcionálanalízis a Hilbert terek és a náluk általánosabb Banach terek, valamint a rajtuk ható operátorok algebráinak elmélete. Ez a matematikának egy olyan ága, amelynek tanulmányozásához meglehetősen sok előismeret szükséges: jártasnak kell lenni a Lebesgue-féle mérték- és integrálelméletben, a komplex függvénytanban, valamint a topológia és az algebra bizonyos területein. A vele való foglalkozás azonban, talán sokszínűségének is köszönhetően, sok élvezetet, szellemi izgalmat jelent. A korábban említett fizikai diszciplínákon túl számos új alkalmazásra is talált, többek között az elektronikus hálózatok, az irányításelmélet, az optimalizálás és a sztochasztikus folyamatok területén.

A funkcionálanalízis alapjainak lerakásában elévülhetetlen érdemeket szerzett a szegedi matematikai iskola egyik megalapítója, Riesz Frigyes, akinek nevét az elmélet számos alaptétele viseli. Tanítványával, Szőkefalvi-Nagy Bélával írt Leçons D’Analyse fonctionnelle könyvük alapművé vált, számtalan kiadást ért meg, és minden világnyelvre lefordították. Szőkefalvi-Nagy Béla legjelentősebb hozzájárulása a Hilbert térbeli operátorok elméletéhez a dilatációs tételén alapuló kontrakcióelmélet kidolgozása volt. Ez az elmélet általános (nem szükségképpen normális), kontraktív (egynél nem nagyobb normájú) operátorokra alkalmazható. A (román származású) amerikai Ciprian Foias-sal közösen elért eredményeiket a Harmonic Analysis of Operators on Hilbert Space monográfiájukban foglalták össze.

Végzésem után, 1975-ben csatlakoztam Szőkefalvi professzor funkcionálanalízis szemináriumához. Kemény munkával sikerült bedolgoznom magam ebbe a tudományterületbe, s pár év múlva megszülettek az első önálló eredményeim, melyek mesterem kutatásaihoz kapcsolódtak. Azóta számos vadászösvényt sikerült vágnom az ismeretlen vadonban, s több értékes trófeát volt szerencsém begyűjteni. Az alábbiakban a Hilbert térbeli kalandjaim pár izgalmas momentumáról szeretnék ízelítőt adni.

A Hilbert térbeli izometriák, amelyek megőrzik a vektorok hosszát, azok közé az operátorok közé tartoznak, amelyeket a legjobban ismerünk. A Neumann – Wold Felbontási Tétel szerint minden izometria egy unitér operátor és egy unilaterális eltolás-operátor ortogonális összege. Az unitér operátorok szerkezetét a David Hilberttől származó, s a normális operátorok diagonalizálhatóságát végtelen dimenzióra általánosító Spektráltétel írja le. A kizárólag végtelen dimenziós terekben fellépő unilaterális eltolások pedig vektorértékű Hardy tereken az identikus függvénnyel való szorzás operátoraként modellezhetők. A szerkezetüket leíró invariáns altereik a Beurling – Lax – Halmos Tétel szerint operátorértékű, analitikus, belső függvények képtereiként jellemezhetők. E tétel alkalmazhatóságát azonban erősen korlátozza, hogy a belső függvényeknek csak 1-dimenzióban ismert, egy Beurlingtől származó, kielégítő paraméterezése. Ennek is tulajdonítható az izometriák invariáns altérhálóinak spektrális jellemzését kérdező, J.B. Conway és T.A. Gillespie által felvetett probléma nehézsége. Az Isometries with isomorphic invariant subspace lattices [J. Functional Analysis, 170 (2000), 475—511] cikkemben az altérhálók izomorfiája esetén fellépő metrikus spektrálekvivalencia igazolása mellett sikerült az izomorfiához szükséges feltételek elegendő voltát is bebizonyítanom a nem-reduktív komponens ciklikussága esetén. Ezzel választ adtam Conway és Gillespie több, 10 éven át nyitott kérdésére.

Bár az izometriákra vonatkozóan is vannak még megoldatlan problémák, ugyanakkor sok operátorokkal kapcsolatos kérdés az izometriák körében könnyen megválaszolható. Ezért lehet nagyon hasznos és célravezető, ha minél általánosabb operátorokhoz tudunk, velük minél szorosabb kapcsolatban lévő izometriákat társítani.

E társított izometriák a legegyszerűbb módon az aszimptotikusan nem-eltűnő, un. C1•-osztályú kontrakciók esetén értelmezhetők. Ilyenkor a T operátor nem növeli meg a vektorok hosszát, s a nem-nulla vektorok T-szerinti pályái nem tartanak nullához. Ezért a T iteráltjainak abszolútérték-négyzeteiből képzett sorozat monoton csökkenve konvergál egy kölcsönösen egyértelmű, pozitív A operátorhoz. Az A segítségével könnyen értelmezhető egy VT izometria és egy a T-t VT-vel összefűző XT kváziaffinitás. A Hari Bercovicivel közös On the spectra of  C11-contractions [Proc. Amer. Math. Soc., 95 (1985), 412—418] cikkünkben megadtuk T és VT teljes spektrális jellemzését a C11-osztályú kontrakciók körében, azaz ha T és az ő T* adjungáltja is aszimptotikusan nem-eltűnő. Az On the spectra of contractions belonging to special classes [J. Functional Analysis, 67 (1986), 153—166] önálló cikkemben ezt a jellemzést kiterjesztettem arra a nehezebben kezelhető esetre is, amikor T C10-osztályú, azaz amikor T aszimptotikusan nem-eltűnő, a T* adjungáltja viszont stabil, ami a vektorpályák nullához való konvergálását jelenti.

Az operátorelmélet talán leghíresebb nyitott kérdései az Invariáns Altér Probléma és a Hiperinvariáns Altér Probléma. Az előbbi azt kérdezi, hogy van-e minden korlátos, lineáris Hilbert térbeli operátornak valódi invariáns altere, az utóbbi pedig azt, hogy létezik-e bármely nem-skalár operátor esetén olyan valódi altér, amely invariáns minden, az adott operátorral felcserélhető operátorra. Ha T C11-osztályú kontrakció, akkor Szőkefalvi-Nagy és Foias egy tétele szerint T kvázihasonló a VT unitér operátorhoz, és VT hiperinvariáns altérhálója beágyazható a T kontrakcióéba. Ugyanakkor a fenti problémák nyitottak abban az esetben, ha T C10-osztályú kontrakció. Izgalmas megválaszolatlan kérdés, hogy mit eredményez ilyenkor a VT izometriával való kapcsolat. Az Injection of unilateral shifts into contractions with non-vanishing unitary asymptotes [Acta Sci. Math. (Szeged), 61 (1995), 443—476] cikkemben bebizonyított általános faktorizációs tétel segítségével megmutattam, hogy ha a VT társított izometria spektrális tartója az egész egységkörvonal, akkor T-nek vannak olyan valódi invariáns alterei, amelyekre való megszorításai unilaterális eltolás-operátorokhoz hasonlók. A J. Functional Analysis folyóiratban megjelenés előtt álló Shift-type invariant subspaces of contractions cikkemben a C1•-kontrakciókra vonatkozó Hiperinvariáns Altér Problémát sikerült az utóbbi speciális esetre redukálnom, amikor is nagyon sok információ áll rendelkezésünkre a kérdéses operátor szerkezetével kapcsolatban.

Szőkefalvi-Nagy Béla a VT társított izometriát egy általánosított Banach limesz segítségével abban az esetben is értelmezte, amikor T aszimptotikusan nem-eltűnő hatványkorlátos operátor. Több cikkemben foglalkoztam az általa alkalmazott eljárás széles körű kiterjesztésével a reguláris norma-sorozatú operátorok tág osztályára. A Tn hatványok normáinak e reguláris viselkedését a Vladimir Müllerrel közös Criteria of regularity for norm-sequences II [Acta Sci. Math. (Szeged), 65 (1999), 131-138] dolgozatunkban teljeskörűen jellemeztük. A Hyperinvariant subspaces of operators with non-vanishing orbits [Proc. Amer. Math. Soc., 127 (1999), 1363—1370] cikkemben a VT társított izometriára támaszkodva sikerült bebizonyítanom, hogy lassú növekedésű teljes vektorpálya létezése esetén az aszimptotikusan nem-eltűnő, reguláris norma-sorozatú T operátornak végtelen sok valódi hiperinvariáns altere van.

A VT társított izometriát nem C1•-osztályú operátorok esetén is értelmezhetjük; ekkor az XT összefűző operátor nullterét a T-re nézve stabil vektorok alkotják. Ezen észrevétel felhasználásával stabilitási tételeket bizonyíthatunk. Nevezetesen, ha a T egy tulajdonságát a köztük lévő kapcsolat révén átörökíti VT-re, s ugyanakkor e tulajdonsággal egy izometria nem rendelkezhet, akkor XT szükségképpen a zéró transzformációval egyenlő, és ezért T stabil operátor. Ily módon sikerült a nevezetes Arendt – Batty – Lyubich – Vu Stabilitási Tételt kiterjesztenem hatványkorlátos operátorokról reguláris norma-sorozatú operátorokra, még általánosabban: kommutatív, diszkrét félcsoportok reguláris norma-viselkedésű reprezentációira. Ez esetben a vektorpályák nullához tartása egy normalizáló sorozathoz viszonyítva, s a G.G. Lorentz által bevezetett konvergencia szerint értendő. Egy doktorandusz tanítványommal ezeket az eredményeket topológikus fécsoportok folytonos reprezentációira is kiterjesztettük.

Azoknak, akik a fenti területtel behatóbban szeretnének megismerkedni, ajánlom, hogy a szükséges előismeretek megszerzése végett először olvassák el a Bevezetés a véges dimenziós vektorterek elméletébe és a Hilbert terek operátorai című jegyzeteimet, melyek a szegedi Polygon Kiadónál jelentek meg. Ugyanennél a kiadónál 2007 végére várható a Valós- és funkcionálanalízis című jegyezetem, amelyet szintén melegen ajánlok.”

ld: Kérchy László: A III. Bélától a Bolyai Intézetig: kalandozások Hilbert terekben. (Tanulmányok a Bajai III. Béla Gimnázium Jubileumára, 1757-2007, Bajapress Nyomda, Baja, 2007, ISBN 978-963-06-5059-7)

Kerékjártó Béla (1898-1946)

Forrás a képre kattintva látható.

Vetsei Kerékjártó Béla  matematikus, egyetemi tanár, a Magyar Tudományos Akadémia tagja (levelező: 1934, rendes: 1944), a topológia és a csoportelmélet nemzetközi hírű kutatója.

 

Vetsei Kerékjártó Károly és Hoecker Berta fia. Budapesten született 1898. október 1-én. Az Újpesti Állami Főgimnáziumban, (ma Könyves Kálmán Gimnázium) érettségizett 1916-ban. A budapesti Pázmány Péter Tudományegyetem Bölcsészettudományi Karán folytatta tanulmányait, és öt félév után engedélyt kapott doktori értekezés benyújtására. 1920-ban avatták bölcsészdoktorrá, magántanári előadásait 1922-ben kezdte meg a szegedi tudományegyetem Geometriai és Ábrázoló Geometriai tanszékén. Ösztöndíjasként többször utazott külföldre. 1922 és 1926 között az egyetemek meghívására Göttingenben, Barcelonában, Princetonban és Párizsban, a Sorbonne-on tartott egyetemei előadásokat a topológiáról és annak alkalmazásairól, a kozmológia matematikai alapjairól, geometriáról és függvénytanról, valamint a folytonos csoportokról.

Az MTA 1934-ben levelező, 1944-ben rendes tagjává választotta, emellett több külföldi matematikai társulat tagja volt. 1945-ben a Magyar-Francia Társaság elnökévé választották.

1935. szeptember 1-tõl Kerékjártó Béla adjunktust is kapott, Lipka István személyében. Sajnos, azonban 1938 nyarán Pestre távozott. Kerékjártó tanszékének vezetését a következõ tanévben Riesz Frigyes látta el, majd 1939. július 19-tõl Szõkefalvi-Nagy Gyulát nevezték ki az egyetem ny. r. tanárává, a Geometria és Ábrázoló Geometria Intézet igazgatójává.

1946 május 26-án hunyt el Gyöngyösön szívgyengeségben, tbc-ben

Geometriai vizsgálatainak kiindulópontja a topológia és a csoportelmélet volt. Sok topológiai alaptétel származik tőle, más tételek igazolását pedig egyszerűsítette. Igen jelentős eredményekre vezetett, hogy a topológiát alkalmazta a matematika más területeinek, nevezetesen a geometriának, a függvénytannak és a csoportelméletnek a tanulmányozására. A topológiai leképezések szerkezetének vizsgálatait egy általa bevezetett fogalommal, a regularitással egységesítette, és újabb eredményekkel gyarapította. A Hilbert-féle axiómarendszer alapján foglalkozott a Bolyai–Lobacsevszkij-síkgeometria új megalapozásával is.


Már 25 évesen ismertté tette nevét Vorlesungen über Topologie című nagyhatású könyvével. Hermann Weyl, századunk egyik Neumann Jánoshoz hasonlóan univerzális nagy matematikusa ezt írta Kerékjártó könyvéről: “… Míg korábban a topológia tudományában a szemlélet alapján történő szigorú bizonyítás kimondottan fáradságos volt, és az ember tizet tehetett egy ellen, hogy ritkán sikerült, Kerékjártó révén ez az út sokkal simább lett, a gondolat és a szemlélet szoros kapcsolatba került. Ezután én is az ő felfogása és elképzelései alapján fogom a topológiát tanítani…”. Szegeden készült el Kerékjártó A geometria alapjai című – később francia nyelven is megjelent – hatalmas monográfiájának első kötete, amelynek hazai publikálásáról így írt a szerző: “… azt a célt kívánom szolgálni, hogy a középiskolai tanár megismerje az általa a középiskolában tanított tételeknek a geometria tudományos rendszerében való helyét …”. Könyvei mellett Kerékjártó nevét mély eredményei is őrzik. A felületek topológiájára vonatkozó vizsgálatain kívül kiemelkedő megállapításokat tett Jordán-görbékről: megmutatta, hogy két Jordan-görbe közötti homeomorf megfeleltetés az egész síkra folytatható, továbbá bebizonyította a klasszikus Jordan-féle görbetétel megfordítását.

  • Vorlesungen über Topologie. Berlin, 1923. 270 p.
  • A geometria alapjairól. 1. köt. Szeged, 1937. 304 p.; 2. köt. Budapest, 1944. 613 p. URL
  • Les fondaments de la géometrie. 1. Budapest, 1955. 340 p.; 2. Paris—Budapest, 1966. 528 p.
  • 1934-ben őt kérték fel az Encyclopédie Francaise topológiai fejezetének megírására

Wikipédia URL

Tudósnaptár URL

Szegedi egyetemi almanach 1921–1970. Szeged; Márta Ferenc – Tóth Károly, 1971. Kerékjártó Béla lásd 173-174. p.

Szegedi egyetemi almanach : 1921-1995. I. köt. (1996). Szeged, Mészáros Rezső. Kerékjártó Béla lásd 333.

Magyar tudóslexikon A-tól Zs-ig. Főszerk. Nagy Ferenc. Budapest: Better; MTESZ; OMIKK. 1997. 453–454. o. ISBN 963-85433-5-3

A Magyar Tudományos Akadémia tagjai 1825-2002. Szerzők: Markó László, Burucs Kornélia, Balogh Margit, Hay Diana. Bp., MTA Társadalomkutató Központ, 2003.

Magyarok a természettudomány és technika történetében. Főszerk. Nagy Ferenc, Nagy Dénes. Bp., MVSZ-MTA-BME-MTESZ-Országos Műszaki Információs Központ és Könyvtár, 1986.

Sain Márton: Matematikatörténeti ABC. 6. kiad. Bp., Nemzeti Tankönyvkiadó-TypoTEX, 1993.

Bognár Mátyás

EMLÉKBESZÉD KERÉKJÁRTÓ BÉLÁRÓL (MTA, 1998)

(Bevezető rész)

Kerékjártó Béla 100 évvel ezelőtt, 1898. okt. 1-jén, Budapesten született, és a matematika több ágára kiterjedő, igen termékeny alkotói évek után 48 éves korában, 1946. május 26-án, Gyöngyösön halt meg.

1920-ban a budapesti tudományegyetemen szerzett diplomát, és ugyanekkor védte meg bölcsészdoktori értekezését is, majd ösztön­díjasként külföldre utazott. 1922 és 1926 között az egyetemek meg­hívására Göttingenben, Barcelonában, Princetonban és Párizsban tartott egyetemei előadásokat a topológiáról és annak alkalmazásairól, a kozmológia matematikai alapjairól, geometriáról és függvénytanról, valamint a folytonos csoportokról.

Hazatérése után 1926-ban nevezték ki a szegedi tudományegyetem Geometriai Tanszékére nyilvános rendkívüli, majd 1929-ben nyilvános rendes egyetemi tanárnak. 1938-tól a fővárosban tevékenykedett – a budapesti tudományegyetem nyilvános rendes tanára volt. A Magyar Tudományos Akadémia 1934-ben levelező, majd 1945-ben rendes tagjául választotta. Több külföldi tudományos társaság tagja volt, és számos külföldi tudományos kongresszuson vett részt. 1933-tól Riesz Frigyes és ő szerkesztették a szegedi Actát.

Kerékjártó Béla három könyvet írt: a topológiáról szóló előadások l. kötetét, valamint A geometria alapjairól című mű I. és II. kötetét. Több mint 70 tudományos dolgozata jelent meg, jó részük rangos nemzetközi folyóiratokban német, angol, francia és olasz nyelven, de számos dolgozatot publikált magyarul is.

Első könyvének bevezetőjéből megtudhatjuk, miről szólt volna a Vorlesungen über Topologie II. kötete. Ez a kötet azonban nem készült el. Nem ritkaság a matematikai irodalomban, hogy egy több kötetre tervezett monográfiának csak az első kötete jelenik meg. Alexandorff és Hopf nevezetes könyve, a Topologie I. kötete egy három kötetre tervezett mű első részeként látott napvilágot.

Kerékjártó munkáit olvasva szembetűnik az a rendkívül széles körű tájékozottság, amely jelen van mind az előző korszakok folyamatait, mind saját korának alkotásait illetően. Tükröződik ez pl. abban is, hogy topográfiakönyvében több oldalon keresztül ismer­teti a végek és a primvégek Canathéodory-féle elméletét, amely a topológiai témájú könyvekben nem szokott helyet kapni.

Kerékjártó írásaiból az is kitűnik, hogy diszkussziókon és levél­váltásokon keresztül igen eleven az a kapcsolat, amely korának számos ismert matematikusához köti. A magyarok közül ebben a vonatkozásban elsősorban Riesz Frigyest kell megemlítenünk, a külföldiek közül pedig Birkhoffot, Brouwert, Knesert, Koebet, Nielsent és Reidemeistert.

Mit is alkotott a matematikában Kerékjártó Béla? Tulajdonképpen nem könnyű a kérdésre a válasz. Topológiakönyvének bevezetésé­ben a szerző utal arra, hogy a tárgyalás elkerüli az aprólékos részle­tezést, különösen ott, ahol ezek a részletek könnyen kiegészíthetők, vagy ahol lényegében már korábban szerepeltek. Ez a munkastílus azonban néhol fontos lépések hiányát eredményezi. A bevezetés arról is szól, hogy a felületek elmélete Riemann 1852-es doktori értekezése és Cantor fellépése közti időszakban inkább experimentá­lis tudományként fejlődött. Kerékjártó láthatólag vonzódik ehhez a kísérleti matematikai korszakhoz, és saját munkássága sem mentes ettől. Ezzel is magyarázhatók helyenként fellelhető tévedései.

Topológiakönyvében például egy szellemes példával önmaga mutatja meg, hogy egy korábbi cikkében publikált egyik állítása téves.

Ily módon biztos választ csak a teljes életmű kritikai feldolgozása után kaphatnánk, és ez a feldolgozás az életmű szokatlan gazdasága miatt nem könnyű feladat. De az életmű részleges áttekintése is azt mutatja, hogy Kerékjártó igen lényeges elemekkel vitte előre korának matematikáját.

Tudományos programját a Szegeden 1921. december 15-én Az analysis és a geometria topológia alapjairól címmel tartott magántanári próbaelőadáson fogalmazza meg. Ebben az előadásban a dimenzióinvariancia-tételt, a tartományjelleg megmaradásáról szóló tételt és Jordan görbetételét a topológia három legfontosabb eredmé­nyének tartja. E tételek közül az első kettő Brouwertól származik.

Hangsúlyt kap az előadásban Brouwer 1910-es habilitációs elő­adásában megfogalmazott azon célkitűzés, hogy a komplex függ­vénytan a topológia eszközeivel épüljön fel (hossz, terület, metrikus elemek nélkül). Ehhez a célkitűzéshez kapcsolódik Kerékjártó ku­tatásainak főiránya: a felületek topologikus transzformációinak és transzformáció-csoportjainak vizsgálata, különös tekintettel a folytonos transzformációcsoportokra.

[…]

A szerző az ELTE nyugalmazott matematikaprofesszora.

Érdekesség:

Somlyó György Kossuth-díjas költő, műfordító így emlékezik Kerékjártó Bélára:

[…] Érettségi után kapcsolatba kerültem Kerékjártó Béla matema­tikussal, akinek előadásait hallgattam az egyetemen. Megláttam egyszer csak az egyetem programjában, hogy Kerékjártó Béla a pro­jektív geometriából tart előadást. No, azt se tudtam, mi a projektív geo­metria, most se tudom már, de rögtön fölkeltette érdeklődésemet, meg aztán érdeklődtem egy kicsit, és megmondták, hogy ez valamiképpen az ábrázoló geometria része, vagy az ábrázoló geometria a projektív geometria része. Ekkor elmentem, és nagyon szorgalmasan jártam egy fél évig. Nagyon érdekelt, bár nagyon keveset értettem belőle egészen biztos, és ma már semmit se tudok belőle, egyetlen egyet kivéve. Ez a Möbius-szalag, ami nekem – mint alapvető metafora -­azóta is megmaradt, és többször használtam is írásaimban.

Emlékszem, Kerékjártó több hétig tárgyalta a Möbius-szalagot, mint ami a projektív geometriának az egyik emblematikus része. és ami az irodalomról akkoriban kialakuló elgondolásaimmal nagyon analogikus volt, metaforikusan, mert ez a két oldal, ami egy oldal. ez megint csak az egész költői masinériának és pláne a for­dítói masinériának egy hallatlanul közeli és érzékletes emblémája, legalábbis úgy, ahogy én felfogtam. Lehet. hogy ahogy fel kell fogni a matematikában vagy a geometriában, úgy nem, de ahogy én felfogtam, úgy igen…. [Möbius-szalagot kapunk, ha egy papír­csíkot, pl. olyant, amelynek egyik oldala színes, összehajtunk és a két végén úgy ragasztunk össze, hogy a színes oldal a fehérrel talá­kozzék. Ennek csak egy felülete van: ceruzával folyamatos vonalat tudunk rajta végigrajzolni.]

Kerékjártó mikor Párizsban járt, elment Valérvhoz, mert ő tudta. hogy Valéry kicsoda, ilyen értelemben is, és Valéry a Füzetek-ben több helyen is említette Kerékjártó látogatását. Abban a kis kötetben. amiben én a Füzetek-nek egy nagyon-nagyon csekély részét lefordítottam magvarra, felvettem első látogatásának leírását. Nagyon érdekelt ez a kapcsolat, és megint csak nagyon elevenné tette az emlékezetemet.

Paul Valéry: Füzetek 1929.

Kerékjártó professzor látogatása, a szegedi egyetemről. Vézna óriás, kétrét görnyedve fejezi ki irántam való tiszte­letét. Fiatal. Nézem ezt a kifejezéstelen. analitikus arcot – a mélyfekete kis szemek tekintetét – és belemerülünk a szakmájába – az Analysis Situs-ba.

Valéryt nagyon érdekelték a matematika és a fizika korabeli eredményei, ezért ezekről sokat olvasott, illetve gyakran személyes ismertség révén szerzett jártasságot olyan tudósok munkáiban, mint Maurice de Broglie. Bernhard Riemann, Michael Faraday, Albert Einstein és James Clerk Maxwel]

 

[Encyclopaedia Britannica]

Forrás: Ponticulus Hungaricus

(Visontay György összeállítása. aki így ír: …. Paul Valéry naplója, a Füzetek számos részlete beleillett Ponticulus Hungaricusba. Somlyó, aki Kossuth-­díja révén tagja a digitális irodalmi akadémiának, megengedte a könyv matematikához, fizikához és biológiához kapcsolódó szövegrészeinek másodközlését. Eközben, szóba került a matematikához való viszonya…”)

Kevei Péter (1984-)

Forrás a képre kattintva látható.

1984. március 25-én születtem Szegeden. Első osztályos koromban a tanító néni év végén megmondta édesanyámnak, hogy matematikus leszek.Ráhibázott. Az első osztályt Szatymazon jártam, majd másodiktól Szegeden a Tarján 4.sz. Általános Iskolában (jelenleg Weöres Sándor Általános Iskola) tanultam. A matematikát szerettem, mert jól ment, de nem nyertem versenyeket, nem foglalkoztam sokat vele. Inkább sakkoztam.A hatodik osztály elvégzése után a szegedi Radnóti Miklós Általános Iskola és Kísérleti Gimnázium matematika tagozatára kerültem. Matematika,kémia és fizika tantárgyakból tanulmányi versenyeken vettem részt. Utolsóközépiskolás éveimben a sakk egyre inkább háttérbe került, és a tanulásra koncentráltam. Matematikatanáraimnak, Mike Jánosnak és Vincze István-nak nagy szerepe van abban, hogy végül matematikusként tanultam tovább.2002-ben Radnóti-díjat kaptam. Ugyanebben az évben érettségiztem kitűnő eredménnyel. Tanulmányaimat 2002-től a Szegedi Tudományegyetem Természettudományi Karán Alkalmazott matematika szakon folytattam. Matematika tagozatosként sem volt fogalmam róla mit csinál egy matematikus. Gondoltam az alkalmazott matematikust biztosan alkalmazzák. Nem tudtam mi szeretnék lenni, viszont a matematikát szerettem. Megfogadtam Édesanyám tanácsát, hogy csináljam amit szeretek. Hamar világossá vált, hogy jól választottam, mindenfajta matematikában megtaláltam a szépséget, leginkább mégis az analízis vonzott. További egyetemi pályámat nagyban meghatározta, hogy 2003 telén egy jól sikerült Valószínűségszámítás elemei vizsga után Csörgő professzor úr meghívott a tavaszi félévben tartott szemináriumára. Ebből egy árva szót sem értettem, viszont a félév végén kaptam egy problémát, melynek megoldásával megszületett első TDK dolgozatom, és ebből lett első matematika cikkem. Csörgő professzor volt a diplomamunkám és a PhD dolgozatom témavezetője is. Sajnos, 2008 februárjában bekövetkezett hirtelen halála miatt csak 4 évig dolgozhattam az irányítása alatt, de ez a 4 év nagyon meghatározta további pályámat, matematikai ízlésemet. Csörgő professzor mind kimagasló szakmai tudásával, mind tanári és emberi magatartásával irányt mutatott az életben. Matematika versenyeken egyetemista koromban is részt vettem. Az International Mathematics Competition for University Students versenyen 2003-ban Kolozsváron, 2004-ben Skopjéban, 2005-ben Blagoevgradban harmadik díjat, 2006-ban Odesszában első díjat kaptam.2007-ben kiváló minősítéssel végeztem alkalmazott matematikus szakon, majd az SZTE TTK Matematika és Számítástudomány Doktori Iskola hallgatója lettem. Csörgő professzor témavezetésével, egy évvel a halála után 2009-ben szereztem doktori fokozatot. Friss doktori fokozattal, témavezető nélkül kicsit elveszettnek éreztem magam. Csörgő professzor barátja, David Mason amerikai professzor segített sokat. David Masonnel azóta számos közös publikációnk jelent meg, valamint többször meglátogatott a világ több pontján. A doktori fokozat megszerzése után határozottan külföldre akartam menni. Kíváncsi voltam, másutt hogy mennek a dolgok. 2009 őszétől egy kiváló mexikói matematikai kutatóintézetbe kerültem. Sok nagyszerű matematikus mellett itt ismertem meg a feleségemet is. Két év után hazajöttem Szegedre, és az MTA–SZTE Analízis és Sztochasztika Kutatócsoportban voltam tudományos munkatárs. 2014-ben elnyertem a Humboldt-ösztöndíjat, amivel 2,5 évet töltöttem a Müncheni Műszaki Egyetemen. 2016-ban Münchenben született Máté fiam. 2017 óta újra Szegeden élek. 2017-ben habilitáltam, utána lettem docens a Sztochasztika Tanszéken, majd 2018-tól tanszékvezető. 2018-ban Alexits György Díjat kaptam, valamint megkaptam a SZTE TTIK Tudományos Díját. 2020-ban született Zoé lányom. Szeretek tanítani. A 2004/2005-ös tanévben kezdtem demonstrátorként kalkulust tanítani. Azóta rengeteg kurzust tartottam különböző szakokon, spanyolul, angolul, legtöbbször azért magyarul. Igyekszem gondolkodásra bírni a hallgatókat, nemcsak gyakorlatokon, hanem előadásokon is. Sokszor nagy ellenállásba ütközöm, de általában sikerül elérni, hogy 4-5 hallgató beszéljen hozzám az órán. A matematika szeretetét próbálom átadni a hallgatóknak. A Bolyai Intézetben sok kiváló előadóm volt. Előadói stílusomra legnagyobb hatással Csörgő professzor előadásai és középiskolai tanáraim, Mike János és Vincze István órái voltak. Általában jó hallgatói értékeléseket kapok, de néha kifogásolják, hogy túl sokat követelek. Évente 2-3 szakdolgozóm, diplomamunkázóm van. Szabadidőmben sakkozom, olvasok, vagy a gyerekeimmel játszom.

/Saját írása/

A születésnap paradoxon


Későbbi mesteremmel, Csörgő Sándor professzorral 2003 őszén, másod-éves koromban ismerkedtem meg. Ő tartotta a bevezető valószínűségszámítás előadást. A legelső óráról pontosan egy órát késtem, mert a kurzus időpontja kedd délután 4-ről 5-re tolódott el valamilyen fizikus órarendi ütközés miatt. Jól értesült hallgatóként én 5 óra előtt pár perccel jelentem meg, viszont Csörgő professzor már 4-kor megkezdte az órát, mivel figyelt arra, hogy a hallgatóság egy része valószínűleg nem értesült a módosításról. Kérdezte, hogy fizikus vagyok-e, majd megkérdezte a nevemet. Miután megmondtam, belenézett a jegyzeteibe, majd közölte, hogy egy napon születtem XY hallgatótársammal. Elég furcsán nézhettem rá, meglepett a dolog. Fogalmam sem volt róla, miről beszél. Aztán világos lett minden. Csörgő professzor a bevezető valószínűségszámítás kurzust nem a valószínűségi mező definíciójával, hanem egy izgalmas feladattal, a születésnap problémával kezdte. Mennyi a valószínűsége, hogy n ember között van kettő, akiknek egy napon van a születésnapja? A meglepő a dologban az, hogy már 23 személy esetén a kérdéses valószínűség 1/2-nél nagyobb. Innen jön a paradoxon elnevezés. Csörgő professzor nem elégedett meg a megoldás ismertetésével, hanem megnézte az ETR-ben a hallgatók születési dátumait, és kiírta az egyezéseket. Miután jobban megismertem, az is kiderült, mennyire jellemző rá ez a részletekbe menő alaposság. Most én is minden bevezető valószínűségszámítás kurzust a születésnap paradoxonnal kezdek. Sajnos a Neptunban a születési dátumok nem nyilvánosak.

Klug Lipót (1854-1945)

Forrás a képre kattintva látható.

Klug Miksa és Neufeld Johanna gyermekeként született Gyöngyösön, 1854. január 23-án. A műegyetem (1870–72), majd a tanárképző (1872–74) hallgatója. 1874-ben ábrázoló geometriai és matematikai tanári oklevelet szerzett. 1893-ig Pozsonyban tanított, majd a budapesti II. kerületi főreáliskolához került. 1882-ben megszerezte a doktori címet. 1897-től az ábrázoló geometria tanára a kolozsvári egyetemen. Ezt a tanszéket Klug számára hozták létre, és az 1917-es nyugdíjazásáig működött. Takarékossági okokból állását már csak a Szegedre menekült egyetemen töltik be újra.

Teller Ede világhírű fizikusnak tizenéves korában alkalma volt találkozni Klug Lipóttal, és azt írta róla, hogy életében ő volt az első felnőtt, aki szerette azt, amit csinált, mert a körülötte élők mindannyian nyűgnek érezték a munkát.

Klug Lipót egy évi nyugdíjából alapítványt hozott létre a kolozsvári egyetemen a tehetséges fiatal matematikusok támogatására. Tízezer pengőt adományozott egykori egyeteme, a kolozsvári Ferenc József Tudományegyetem matematikai és természettudományi karának, hogy a tehetséges diákokat anyagilag támogassák. Az ösztöndíjat azonban csak 1943-ban adták át. Nyertesei Zigány Ferenc és Fejes Tóth László voltak, 1944 és a román megszállás véget vetett az alapítvány működésének.

Tévesnek bizonyultak azok a feltevések, hogy 1944 őszén, a zűrzavaros időkben véglegesen eltűnt volna. Az életrajzokban mindenütt ez szerepel. De 1945 januárjában előkerült a bujdosásból, és március 24-én halt meg, 91 évesen. A budapesti Kozma utcai zsidó temetőben nyugszik (5B parcella 10. sor 13. sír).

Házastársa Guttmann Sarolta (1857–1941) volt, Guttmann Lipót és Brasch Mária lánya, akivel 1878. januárjában Gyöngyösön kötött házasságot.

Az ábrázoló és szintetikus projektív geometria. Ebben a témában az egyik legnagyobb hatású és legtermékenyebb magyar matematikus volt.

  • Projektiv geometria, Az MTA anyagi támogatásával, Lampel Robert (Wodianer F. és fiai), Budapest, 1903.
  • A projektiv geometria elemei (Synthetikai-geometriai módszerrel), Az MTA segélyezésével, Franlkin-Társulat, 1892.
  • Az általános és négy különös Pascal-hatszög configuratiója, Ajtai K. Albert, Könyvnyomdája, Kolozsvár, 1898.
  • Ábrázoló geometria, A reáliskolák VI., VII. és VIII. osztálya számára a legújabb tantervnek megfelelően, Lampel Robert (Wodianer F. és fiai), Budapest, 1900.
  • Az egyszerű görbe felületek ábrázolása, Kolozsvár, 1909–10. (kézírásos, sokszorosított egyetemi jegyzet)
  • Perspectiv helyzetű alakzatokról, Budapest, 1882. URL
  • Klug Lipót Wikipédia URL
  • Oláh-Gál Róbert: Klug Lipót (1854–1945), Matematikai Lapok, 18, 1 (2012) 11–25.
  • Zigány Ferenc: K. L. Matematikai és Fizikai Lapok, 1943.; 
  • Kárteszi Ferenc: Találkozásaim K. L-tal. Matematikai Lapok, 1973.
  • John J. O’Connor és Edmund F. Robertson írása, Klug Lipót a MacTutor archívumban.
  • MacTutor Leopold Klug URL

Klukovits Lajos (1944-)

Forrás a képre kattintva látható.

Szegeden születtem, 1944. október 8-án. (e napokban haladt át a II. világháború frontja Szegeden.) A mórahalmi általános iskolában kezdtem tanulmányaimat 1951-53 között. 1953-59 között a Tanárképző Főiskola I.sz. Gyakorló Általános Iskolájába jártam (ezen iskola épületében volt matematika-természettan- ének-zene szakos tanár az 1920-as évektől 1937-ig anyai nagyapám, Klacskó Győző.) 1959 és 1963 között a Radnóti Miklós Gimnáziumba jártam, utána a József Attila Tudományegyetem Természettudományi Kar matematikus szakon végeztem 1968-ban.

/Saját írása/

1968-2014 között ugyanaz, csak a neve változott: JATE majd SZTE Természettudományi majd Természettudományi és Informatikai Kar Bolyai Intézet Algebra és Számelmélet Tanszék, végighaladtam a ranglétrán a gyakornoktól a docensig; 2015-től címzetes egyetemi tanár lettem.

/Saját írása/

Univerzális algebra, egy korai eredményem az 1990-es évektől kiterjedt alkalmazásra került, igen sok dolgozatban idézték/idézik, egy konstrukcióját több hivatkozásban nevemmel illetik;

2000-től több matematika történeti dolgozatot is publikáltam

1973: egyetemi doktori cím (témavezető Csákány Béla)

1987: kandidátusi fokozat (témavezető Csákány Béla és részben Schmidt E. Tamás)

/Saját írása/

Az általános iskola V. osztályában félévkor négyest kaptam matematikából nyilván jogosan, mert már akkor is sok számolási hibát vétettem. De az ilyen jegy szokatlan volt számomra, amit tetőzött, hogy tanárom nem akarta megengedni, hogy induljak az iskolai matematika versenyen. Ezt azért sikerült kivívnom, és dacosan versenyezve nemcsak azt, hanem a városit is megnyertem. A következő évben új tanárom lett, aki végleg megszerettette velem ezt a tárgyat. Ő Kálmán Mihály volt, aki pár év múlva átkerült a vasútforgalmi technikumba, ahol hosszabb ideig tanított még. Ezután már szinte egyenes volt az utam, amit az sem akadályozott, hogy a gimnáziumi matematika tanárommal enyhén szólva is bonyolult volt a viszonyom (nem igazán kedveltük egymást). Megint előjött dacom, és szakkörvezető tanáraim segítségével, a KÖMAL feladatain edződve haladhattam tovább. Egy időben elméleti fizikus akartam lenni, de erről letettem, és matematikus szakra jelentkeztem.

Egyetemi éveim alatt Csákány Béla és Szőkefalvi Nagy Béla előadásai voltak legnagyobb hatással, de az utóbbi professzoréi inkább csak az igen logikus fölépítések révén. Az algebrát Csákány Béla kedveltette meg velem.

Egy kis kitérő: A 60-as években a JATE 3 karának csapatai között nagy nézőközönség előtti ún. szellemi öttusa versenyek voltak. A csapatokba (általában 5 fő) karon belüli vetélkedők eredményei alapján lehetett bekerülni. II. éves koromtól kezdve minden évben bekerültem a kar csapatába, és rendszerint a TTK csapata nyerte meg az egyetemi versenyt. Rajtam kívül még egy matematikus hallgató volt a csapatban, Krámli András, egy igazi reneszánsz műveltségű hallgató. A csapatunkat az egyetemi versenyekre Pollák György matematikus kutató készítette föl, aki országos/TV-s műveltségi versenyeket is nyert abban az időben. Az ő rendkívüli általános műveltsége is nagyon nagy hatással volt rám.

/Saját írása/

Az algebra és a számelmélet területén előbb gyakorlatokat vezettem, majd előadásokat tartottam elsősorban tanár szakos hallgatóknak. Bevezető algebra kurzusomhoz jegyzetet is írtam. Hosszú időn keresztül voltam gazdája (egy évig gyakorlatvezetőként, majd sok évig előadóként) az informatikus hallgatók Diszkrét matematika kurzusának (ehhez én írtam az egyik első jegyzetet).

Pollák György a 80-as évek végén rám hagyományozta a tanárjelöltek matematika történeti kurzusát. Az évek során — követve tanácsát — egyre inkább növeltem az előadásokban az általános kultúrtörténeti tartalmat. Így alakult át az egyszerű matematika történet kurzus a mai Fejezetek a matematika kultúrtörténetéből cíművé, amely hűen tükrözi az átalakult tartalmat.

/Saját írása/

Az 1990-s évektől két ciklusban a Bolyai Intézet vezető-helyettese voltam és két részletben 4 alkalommal választottak meg általános és tudományos dékán-helyettesnek. E pozícióban összesen 11 évig szolgáltam.

1993-től részese voltam az átalakuló tudományos továbbképzési/fokozatadási rendszer kialakításában, a doktori iskolák megszervezésében, akkreditációjában mind kari mind JATE szinten. 1998-ban kezdeményezésemre alakította meg a JATE Szenátusa a JATE Doktori Intézetét, amely 2000-től mint az SZTE ugyanilyen intézeteként működött. Ennek vezetésében nyugdíjazásomig vettem részt 2009-ig igazgatóként. E tevékenységem volt a fő indoka annak, hogy 2009-ben megkaptam a Magyar Köztársaság Lovagkeresztje kitüntetést.

/Saját írása/

Gimnáziumi éveimben kezdtem el versenyszerűen sportolni. Elsősorban sprinter voltam, de harmadikos koromtól kosárlabdáztam is. Komoly eredményt 4×400-as váltó tagjaként értem el: az Országos Középiskolai Atlétikai bajnokságon bronzérmet, az Országos Sportiskolai Bajnokságon ezüstérmet nyertünk. Sajnos egyetemi éveimben már választanom kellett az intenzív sportolás és a tanulás között, nyert az utóbbi.

Anna lányom gyógyszerész kutató, PhD fokozata van.

/Saját írása/

Klukovits Lajos Videotorium URL

Délmagyar: A matek kultúrtörténete – A reneszánsz festészettől a geometriáig URL

Kosztolányi József (1963-)

Forrás a képre kattintva látható.
  1. 03.11. Kossuth rádió, “Nagyok” c. műsor, Beslin Anita riportjának jegyzete

Szegváron, majd Szentesen járt általános iskolába. Tanulmányait tanárai javaslatára a szegedi Radnóti Gimnázium matematika tagozatán folytatta, itt is érettségizett. Már kis gyermekkorában is gyakran játszott „tanárosat”: úgy tűnik, mindig is tanár akart lenni. A matematika-fizika szak elvégzése után – nagy örömére – egykori iskolája, a szegedi Radnóti Gimnázium hívta meg tanítani. Sok éven át tanította matematikára az okos gimnazistákat. Több diákja is komoly eredményeket ért el országos és nemzetközi matematikaversenyeken.    A Mozaik Kiadónál több, társszerzőkkel írt matematika tankönyve jelent meg – a Sokszínű matematika tankönyvsorozat – mely éveken keresztül piacvezető volt a középiskolák körében. Mind tartalmi, mind formai, mind módszertani szempontból tetszett a diákoknak is, a tanároknak is. 

Kedves tanára, Pintér Lajos 1993-ban hívta meg a Bolyai Intézetbe az Analízis Tanszékre a matematika szakmódszertan és más tanári kurzusok tartására. A Radnóti Gimnáziumtól nem könnyen szakadt el, óraadó tanárként még hosszú évekig tanított a speciális matematika tagozaton. Jelenleg is foglalkozik középiskolásokkal, „olimpiai” (nemzetközi matematikaversenyekre, többek közt a Nemzetközi Matematikai Diákolimpiára felkészítő) szakkört vezet. Ez a szakkör kiemelt tehetséggondozó munkát jelent. Egy-egy szakköri foglalkozásra még manapság is 5-6 órát készül. Önálló feladatmegoldásra, sőt, probléma-felvetésre neveli tanítványait, de az angol nyelvű szakirodalom olvasása is a képzéshez tartozik.

A riportban külön hangsúlyozta, hogy a matematika szép, méghozzá olyannyira szép és tökéletes, hogy valójában a legszebb formulái, tételei „Istenbizonyítékok”.

Saját bevallása szerint sosem unatkozik. Hogy ez még véletlenül se következhessék be, már fiatal korában elkötelezte magát a színház, a színjátszás mellett. A tanár- és színész lét közös vonása az állandó tanulás, és az állandó „fellépések”, hol a színpadon, hol a katedrán. Ez együtt jár némi lámpaláz folyamatos átélésével. Határozott véleménye, hogy csak addig szabad két hivatását folytatnia, amíg órái, illetve fellépései előtt érzi ezt az ösztönző izgalmat.

Első színházi „lépéseit” még középiskolai diákként a Szegedi Ifjúsági Színpad tagjaként kezdte, ma már profi színészként ismerik. Sok kedvenc szerepe közül kiemelkedik a 12 dühös ember 3. esküdtje, Szindbád a Krúdy Gyula novelláiból készített előadásban, de játszotta már Szent-Györgyi Albertet is. A színészi hivatással nyilván természetesen együtt jár az irodalom, az olvasás szeretete is. Ha még ehhez az egészhez további hobbikra van szüksége, akkor ott a sport és a zene.



Horváth Eszter interjúja URL

Új docensünk: dr. Kosztolányi József 

Sokan úgy gondoljuk, fontos hír, hogy a Bolyai Intézetben a matematika szakmódszertan oktatóját, dr. Kosztolányi Józsefet docenssé léptették elő nemrégiben az SZTE TTIK Bolyai Intézetében. Felsőoktatási Tanulmányi Emlékérem, kitüntetéses oklevél, Graphisoft-díj, illetve Beke Manó Emlékdíj tulajdonosa. Matematika szakmódszertanból PhD fokozatát Debrecenben szerezte. Óraadóként folyamatosan tanít a szegedi Radnóti Miklós Gimnáziumban. Őt magát személyesen is nagyon sokan ismerik, tankönyveit, feladatgyűjteményét még többen, ám valószínűleg mindenkinek mond újdonságot is az alábbi beszélgetés. – Örülök, hogy sikerült egy kis időt szakítani a beszélgetésre gimnáziumi óráid után. Milyenek voltak ma reggel a diákok?

2 – Kicsit bambábbak a kelleténél (tanítási szünet utáni első napon), de 5-10 perc alatt be lehetett őket mozgatni. Zömében elkészítették a házifeladatot, először azt beszéltük meg, itt a tizedikes osztályban én csak katalizáltam a háttérből. Utána logaritmusos egyenlőtlenségekkel foglalkoztunk. – Hogyan hasznosítod középiskolai tapasztalataidat a tanárjelöltek felkészítésében? – Szakmódszertan előadáson mindig elhangzanak az adódó tanulási szituációk, amelyek elemezhetők. Fontos, hogy tudom, hogy egy-egy helyzetben a gyerekek hogyan reagálnak. Van, amikor a tanár nem is érzi, hogy a tanítandó anyag nehéz. A gyerekek reakcióiból azonban kiderül, hogy pontosan mi is nehéz. Megbeszéljük, hogy milyen ötletek segíthetnek ilyenkor. – Egyáltalán miért fontos szakmódszertant tanítani? Nem elég, ha a tanárjelölt csak a matematikát tudja nagyon jól? – Természetesen, ha adottak a tanítási tartalmak, akkor azokat nagyon jól kell tudni. De olyan felépítésben kell a tudást átadni, hogy az a lehető legkönnyebben elsajátítható legyen. Lehet persze a geometriát az Elemek alapján is tanítani, de nem a leghatékonyabb. Matematika esetében leginkább az irányított felfedeztetés működik a legjobban, középiskolában biztosan, de ez bizonyos mértékben a felsőoktatásra is igaz. A szakmódszertani előadások kétharmada arról szól, hogyan építhető fel egy anyagrész az életkornak is megfelelően. Absztrakt matematikai fogalmakat építünk ki, amelyeknek mindig kell, hogy legyen tapasztalati alapja matematika esetében. – Középiskolában is, és egyetemen is tanítasz. Nehéz-e a váltás a kettő között? – Kicsit igen. Fontos különbség, hogy középiskolában számottevőbb a tanár nevelő funkciója: a fegyelmezés, illetve a figyelemre szoktatás. A matematikát tekintve az a leglényegesebb, hogy negyedéves hallgatóban van kiépített rendszer, a középiskolában pedig ez az építkezés zajlik. Az egyetemen a felülről látást kell megteremteni.

3 – Mennyiben tudtál alapozni Duró Lajosné munkásságára, és miben kell alkalmazkodnod a megváltozott körülményekhez? – Jól tudtam rá alapozni. Kezdetben párhuzamosan dolgoztunk, én az előadást tartottam, ő a gyakorlatot. Természetesen az általa összegyűjtött anyag az akkori oktatási szemléletet képviselte, amit azóta már sok tekintetben tovább kellett fejleszteni. Ma már például sokkal pragmatikusabban kell tanítani, az alkalmazások nagyon fontosak. – Mire kell szerinted felkészíteni ma egy tanárjelöltet? – Jó lenne, ha szeretné a tárgyat, amit tanítani akar. Legyenek intellektuális élményei: állandó önképzésre, olvasásra kell szoktatni őket. Szeretniük kell a gyerekeket, akkor is, ha butuskák, és akkor is, ha kimagaslóak, de nagyképűek. Úgy próbáljanak tanítani, hogy pozitív élmény is érje a tanítványokat, ne csak frusztráció.

4 – Matematikát nem lehet tekintélyelven tanítani, legalábbis az öndefiniált tekintély nem elegendő. A jó tanár tud, emberséges, és módszertanilag is felkészült. – Hogyan tartod a kapcsolatot tanárkollégákkal? – Nagyon sok tanárt személyesen is megismertem az elmúlt évek alatt. A Bolyai Társulat Oktatási Szakosztálya elnökeként szervezője vagyok a Rátz László Vándorgyűléseknek. Rendszeresen járok iskolákba előadást tartani, imádok idegen gyerekekkel foglalkozni, mindig érdekes kihívás, hogyan tudom őket bemozdítani. Rendszeresen találkozom kollégákkal a tehetséggondozó táborokban is. Megemlíteném még a szentesi Tudás 10 napja című rendezvényt. Szívesen tanulok jó tanároktól, és ha látok egy kiváló órát valahol, szívesen hasznosítom a tapasztalatokat. – Kiktől tanultál legtöbbet, kiket tekintesz mestereidnek? – Nagyon sokat tanultam Pintér Lajostól, formálisan és informálisan is. Surányi Jánostól, aki látta óráimat, elemezte, sokat leveleztünk is. Hajnal Imrétől, Szendrei Juliannától, Pósa Lajostól. Németh Józseftől, bár hozzá hivatalosan semmilyen kurzusra nem jártam, de láttam előadásait, óráit; a sokak által jól ismert szemlélete, a tanításhoz való viszonya természetesen rám is nagy hatást gyakorolt. Cofman Juditot is megemlítem, aki Debrecenben a didaktikai PhD programnak volt a vezetője. Természetesen, mint minden tanár, a tanítványaimtól, az ő reakcióikból is tanultam, hiszen a tanítási folyamat mindig egy odavissza működő kibernetikai rendszer. – Családod? – Feleségem matematikatanár, szintén a Radnóti Miklós Gimnáziumban. Máté fiam közgazdásznak készül, a két kisebb gyermekem még általános iskolás. Velük kapcsolatban is fontos célkitűzésem, hogy szeressék a matematikát, ezért sohasem mondom nekik, hogy nem érek rá. Ez még most működik

5 – Mivel foglalkozol a nyilvánvalóan nagyon kevés szabadidődben? – Hetente kétszer focizni szoktam a Radnóti Gimnázium tanáraival. Ezenkívül 17 éves korom óta tartó nagy szerelem az amatőr színház, ahol szervezek, rendezek és szerepelek is. – Terveid a jövőre nézve? – Tankönyv és feladatgyűjtemény írásában vagyok, de foglalkoztat az is, hogyan lehetne a felsőoktatásban hatékonyabbá tenni az alapozó tárgyak tanítását, egyfajta deduktív rendszerben. Olimpiai szakkört tartok kéthetente egy nagyon tehetséges középiskolás csapatnak, ezt szeretném mindenképpen folytatni. Ezen kívül szeretnék részt venni az új matematika érettségi részletes szakmai elemzésében, témakörönkénti mélységű adatelemzések készítésével. Ez szerintem hasznos információ lenne, hogy a későbbi döntéshozatalokban ne az indulatok, hanem az adatok beszéljenek. -Köszönöm a beszélgetést! 

Horváth Eszter

  • Nagyok Kosztolányi Józseffel URL
  • Az ember nem bújhat ki mögüle – interjú Kosztolányi Józseffel: készítette Kósa Boglárka (2020. szeptember 04) URL
  • Horváth Eszter interjúja URL
  • Kosztolányi József: ˝A színházhoz racionalitással kell közelíteni, pont, mint a matematikához˝ URL
  • Kosztolányi József Port URL

Kozma József (1959-)

Geometria tanszék

főiskolai docens

Tudom, nem tipikus önéletrajzi fordulat, hogy otthonon kívüli életemet 14 éves koromtól lényegében ugyanabban a házban élem.

A Szegedi Tanárképző Főiskola 1. sz. Gyakorló Általános Iskolájából a JATE Ságvári Endre Gyakorló Gimnáziumába felvételiztem speciális matematikai tagozatra. Bár gimnáziumi osztálytermünk eleinte a Hősök Kapujában a Díszterem fölött volt, a negyediken, a természettudományos órák az akkori B épületben, a volt Piarista gimnáziumban voltak, amelynek nagyobbik részét akkor is a Bolyai Intézet és a TTK Dékáni hivatala foglalta el. Kiváló matematikatanáraim voltak, Horóczi Ferenc, aki a szisztematikusságra, gondosságra, a fegyelmezett gondolkodásra nevelt bennünket, és Kállai István, aki annyira szerette a geometriát és az operát, hogy ezzel egész életre szóló hatással volt rám.

Tanár szüleim is zenekedvelők voltak, magam is jártam zeneiskolába, és énekeltem kórusokban. Így azután nagyon jó helyem volt a Ságváriban. Innen a JATE matematika-fizika szakára felvételiztem 1998 tavaszán, így azután 1979-ben, egy év katonai szolgálat után ugyanabban az épületben találtam magam, csak most már az Aradi vértanúk tere felőli főlépcsőházba léptem be naponta. Voltak ismerősök a tanáraim között, Pintér Lajos és Gehér László tanár urak, akik a gimnáziumi évek alatt vezettek nekünk szakköröket. Mivel szüleim 25 évvel korábban ugyanerre a szakra, ugyanide jártak, itt ismerkedtek össze, izgalommal vártam a találkozást az otthon gyakran emlegetett Szőkefalvi-Nagy Bélával, Tandori Károllyal, és valamikori csoporttársukkal, Csákány Bélával.

Öt év elteltével, 1984-ben, Nagy Péternek, a Geometria tanszék vezetőjének a hívására lettem tudományos segédmunkatárs ezen a tanszéken, és még mindig ugyanabban a tekintélyt parancsoló házban, ahol most is dolgozom.

Igaz, időközben láttam sokféle más Házat is, a helyi politika révén jól ismerem belülről a szegedi Városházát, nyolc évet szolgáltam képviselőként az ország házában, az Oktatási bizottság tagjaként és a Külügyi bizottság alelnökeként megismertem a világban sok más oktatási-kulturális és politikai rendszert, Strasbourgban és Brüsszelben szívtam magamba az “európai levegőt”. Ezen időszakból egy nagyon szép dolog mind a mai napig folyamatosan megmaradt (most is csak a pandémia miatt szünetel): kapcsolatom az énekléssel, azóta is tagja vagyok a Szená-Torok kórusának.

Mi matematikusok olyan munkát végzünk egyetemi oktatóként és kutatóként, amelyet nagyon szeretünk. Életünknek döntő részét ez időben is lefoglalja, kitölti. Így azután különösen fontos és érdekes, ha magán-, civil életünkből megmutathatunk valamit ugyanebben a közegben.

A matematikai alkotás és az oktatás is kinek-kinek az egyéni teljesítményeként jelenik meg a szakmai körök, illetve a hallgatóság megítélésében. Miközben pontosan látjuk és tudjuk, hogy rengeteget számít a közeg, a hely, ahol a teljesítmény sok-sok munka, a tehetség és szorgalom révén létrejön. A Bolyai Intézetben a hallgatói évek lezárulta után is nap mint nap valami új ismeretre, inspirációra tesz szert az ember, amiről tudományos publikációiban, kollégái előtt az Intézet szemináriumain, konferenciákon számot is adhat.

A matematikusokról az járja, hogy nem állnak távol a kultúrától, különösen a zenétől. Abban biztosak lehetünk, hogy a városi zenei események, komolyzenei koncertek, operaelőadások látogatói között magasan felülreprezentáltak vagyunk.

Az Intézet világában mindez néhány éve valami egészen különleges módon öltött testet.

Tízegynéhány munkatárs belevágott egy vállalkozásba: az évzáró karácsonyi esten énekelni fogunk, hozzájárulunk a közös alkalom meghittségéhez. Az ötletet köremailek követték, és hamar kiderült, hogy sokaknak van olyan zenei (elő)képzettsége és gyakorlata, hogy egy tucat ember össze tud állni négyszólamú kórusművek megszólaltatására. Professzoroktól tanársegédig, együtt a saját könyvtárunk és az intézeti iroda kolléganőivel. Olyan emberek, aki mindennapjaikban ahhoz vannak szokva, hogy csak a legjobbal, hibátlannal lépjenek a (szakmai) közvélemény elé, mire is vállalkoztak? Saját kollégáik, munkatársaik elé állnak oda egy saját maguk által létrehozott közös produkcióval! Amely biztosan nem lehet a legjobb kóruselőadás, és természetesen lehetnek benne hibák.

De valamiben biztosan a legjobb: a művészet, a zene, az alkotás tiszteletében, a szorgalomban, a saját munkatársak és a kollektíva irányában megnyilvánuló szeretetben.

Első alkalommal 2016 novemberében indultunk, karácsonykor már kedves kis karácsonyi dalokat énekeltünk el, rá egy évre Kodály Zoltán Adventi énekével rukkoltunk elő. Azóta sok szép órát töltöttünk együtt számok tanulásával, Nagy-György Judit vezetésével. Azóta énekeltünk még háromszor az évzárónkon, és köszöntöttük Hatvani László és Móricz Ferenc professzor urakat jubileumukon.

Az évek során nagyon sok hallgatóval, oktatóval kerültem kapcsolatba. Bevallom, újabb és újabb ismerőseimet azzal a kíváncsisággal fürkészem, vajon az ő pályájukon miféle gazdag és színes fordulatokat hoz az élet, ők egy rendhagyó életrajzban vajon mire térnek majd ki?

 

Szeged, 2021. március 14.

Kozma József

/Saját írása/

Krámli András (1943-2019)

Forrás a képre kattintva látható.

Krámli Andás 1943 április 14.-én született Szegeden. A Radnóti Miklós Gimnáziumban érettségizett 1961-ben, majd a Szegedi Tudományegyetemen szerzett matematikus diplomát 1966-ban. Különösen nagy hatással volt rá a Szőkefalvi Nagy Béla professzortól tanult funkcionálanalízis. Ezt követően a Magyar Tudományos Akadémia Számítástechnikai és Automatizálási Kutatóintézetének  (MTA SZTAKI) munkatársa lett. 1970-ben osztályvezetője, Arató Mátyás kezdeményezésére a moszkvai Lomonoszov Egyetemen lett aspiráns a Kolmogorov-tanítvány Ya. G. Sinai témavezetésével. Itt Geodetikus áramlások fokális pont nélküli Riemann felületeken c. kandidátusi értekezését 1973-ban védte meg. (Sinai a világ vezető matematikus egyéniségeinek egyike, a legrangosabb díjakban − többek között Wolf- illetve Abel-díjban részesült.)

 Krámli András 1991-ben lett a matematikai tudomány akadémiai doktora.

1990-ben hazatért a Szegedi Tudományegyetemre, az Analízis Alkalmazásai, később Szochasztika Tanszékre.

Ekkortól itt tanított valószínűségszámítást és matematikai statisztikát, majd 1994-ben ide nevezték ki egyetemi tanárnak. 1998-tól 2014-es nyugdíjba vonulásáig a matematikus szakon ő tartotta a matematikai statisztika, sztochasztikus folyamatok, idősor analízis és kockázati folyamatok előadásokat és gyakorlatokat is. Számolatlan diplomamunkázója mellett, vezetésével ketten szereztek PhD fokozatot. (Szepesvári Csaba 1999-ben, és Szakálné Kanó Izabella 2012-ben)

Statisztikai következtetések elmélete című, Bolla Mariannával közösen írt egyetemi tankönyve 2005-ös megjelenését követően 2012-ben már második kiadását éli. Osztálytermi tanári munkájánál hovatovább fontosabb, hogy Krámli professzor egyetemre kerülésével megtalálta természetes életközegét: szinte együtt élt a matematikus hallgatókkal és az intézet összes doktoranduszával, mindenkit a helyzetnek megfelelően buzdítva, vigasztalva, bármely tárgyból korrepetálva és órán kívül is állandóan matematikára tanítva. Krámli András nyugdíjba vonulásával sem szakadt el az egyetemtől, hiszen minden félévben tartott kurzust mesterszakos hallgatóknak. Örökös segítőkészsége, önzetlensége és áldozatvállalása, szerteágazó műveltsége, valamint közvetlen és rendkívül szerény kedves személyisége miatt hallgatóink közszeretetének örvendett.

Legfontosabb kutatási területe a statisztikus fizika és az ergodelmélet, melyben jelentős eredményeket ért el. Úttörő eredménye a 3, illetve 4 golyóból álló kemény golyórendszerek ergodikus és keverő tulajdonságának igazolása, mely Szász Domokossal és Simányi Nándorral közös. Szász Domokos, Fritz József és Major Péter akadémikusokkal, Krámli András a statisztikus fizika nemzetközi rangú magyar iskolájának megalapítója.

Ugyanakkor Krámli professzor kutatási területe nemcsak az elméleti matematikára koncentrálódik, hanem a gyakorlati alkalmazásokban is jelentős eredményeket ért el. Foglalkozott számítógépes eljárások, orvosi és mezőgazdasági folyamatok valószínűségi modellezésével és statisztikai vizsgálatával is. Krámli András 47 tudományos dolgozat és egy egyetemi tankönyv szerzője, 5 tudományos monográfia szerkesztője.

                                                 

Krámli András személyében különleges nagy és széles műveltségű, a matematika és a kultúra sokféle kivételes teljesítményét ismerő, azok iránt lelkesedni tudó és lelkesedést ébreszteni tudó, mélységesen emberi kollégát, illetve barátot vesztett a hazai matematikus társadalom 2019 január 24-én.

Kitüntetései: 1984-ben az MTA Akadémiai Díjjal tüntette ki Fritz Józseffel,  Major Péterrel és Szász Domokossal együtt a matematikai statisztikus fizika modern elméletének hasznosításáért és az ebben elért, nemzetközileg elismert, kiemelkedő eredményeikért

 Szász Domokos írja nekrológjában: „16 közös dolgozatunk három szakaszban született. Az 1979-től 1985-ig tartó elsőben a Sinai-biliárd elméletét tanultuk oly módon, hogy a síkbeli Lorentz-folyamat különböző sztochasztikus tulajdonságait igazoltuk Bunimovich és Sinai Markov-felbontására alapozva. Az 1983-tól 1987-ig tartó másodikban belső állapotú bolyongások hasonló tulajdonságait vizsgáltunk, 1986-tól már Simányi Nándorral is közösen. Végül az 1989-től 1992-ig tartó harmadikban először sikerült félig-szóró biliárdok ergodicitását bizonyítanunk, ami már a Sinai-bilárd misztériumában volt szenzációs eredmény. Ezzel alapoztuk meg a Boltzmann-Sinai Ergodikus Hipotézis igazolását. Hármasban 3 ill. 4 golyóra sikerült ezt megtennünk. (A moszkvai iskola csak 2 golyóra mutatta meg az ergodicitást; ez a rendszer teljesen szóró biliárddal izomorf. Végül 2013-ban Simányi Nándor teljes általánosságban is sikerrel járt!) Az első két szakaszban igen sokat segített András „funkanal kultúrája” és hasonlóan az elsőben és harmadikban mindaz, amit Moszkvában tanult a hiperbolikus dinamikai rendszerekről. Konkrétan egyrészt perturbációelméletet és operátor polinomok spektrálelméletét, másrészt a sima hiperbolikus dinamikai rendszerek elméletét alkalmaztuk (a Sinai-biliárd egyik fő nehézsége, hogy a dinamika nem sima, hanem szakadásos, és tágítása sem korlátos.)

András büszkén írta ki honlapjára Sinai idézetét:

Look Andrash, there are everywhere phase transitions! 

Ya. G. Sinai

 

Mint említettem, 1990-től tért vissza szülővárosába az Egyetem Sztochasztika Tanszékének professzoraként. Itt alapítója volt a Bolyai Intézet doktori programjának, továbbá a Gazdaságtudományi Kar doktori iskolájának is. Éveken át volt az Országos Akkreditációs Bizottság Matematikai Szakkollégiumának tagja.

Ehhez csak annyit tehetek hozzá, hogy mi is ilyennek ismertük. András mindannyiunknak mélyen hiányzik és hiányozni fog.”

In memoriam: Krámli András 

Egy egyetemi kirándulás során ismertem meg személyesen Andrást. Igen, Andrást, és nem a professzor urat, ugyanis a kiránduló diákok mindaddig tegezhették őt, amíg a túrára induló társaság célba érkezés szerinti mediánjánál ő hamarabb ért a csúcsra.„1943. április 14-én születettem Szegeden a Fogklinikán.”Azon a klinikán, ahol ma a Fogászati Klinika üzemel. A születésnap igencsak érzékeny téma Andrásnál, nem ünnepelte, sőt mi több egyenesen leszidta azokat, akik felköszöntötték. „Köszönöm, bár tudod, hogy nem tartom, ha meg akarod ünnepelni, meghallgatsz egy áriát a Don Giovanniból (Youtube, pl. “Batti batti bel Masetto”).”Nem meglepő, ez volt a kedvenc darabja. Ha mindenképpen egy dátumra szeretnénk emlékezni, – javasolta – a születésnapja helyett legyen ez 1787. október 29., a Don Giovanni prágai debütálása. Életének minden évtizedében legalább egyszer megtekintette, kívülről énekelte az áriák minden sorát, természetesen olaszul. Jól tudták ezt diákjai is, így 70. születésnapján, ami éppen egy kirándulás idejére esett, a Prédikálószék csúcsára érve lejátszottuk neki. Örömében annyira átadta magát a darabnak, hogy egyes jeleneteket ő maga játszott el nekünk. A képek magukért beszélnek. Ezen kirándulások hagyományáról ejtenék pár szót.

Az elmúlt 30 évben, szemeszterenkéntegy alkalommal az ország valamely pontján szegedi matematikus hallgatók, egykori hallgatók és oktatók túrára indulnak. A helyszín és a társaság idővel változik, de ezeknek az alkalmaknak az egyik közös pontja András volt. Éjjeli előadást tartott változatos témákról, ami éppen foglalkoztatta, eszébe jutott, amit a diákság számára érdekesnek, hasznosnak ítélt. Ugyan a hallgatóságot este 10 óra és néhány pohárka után kihívást jelentett ébren tartani, ez nem volt kifogás. Az anyag előre kidolgozott posztereken érkezett a szállásra, gondosan feltekerve, újságpapírba csomagolva, utazótáskára felrögzítve, már csak a helyét kellett megtalálni. Láttuk faliújságra tűzve, ajtóra ragasztva, függönykarnisra akasztva. Az egyik alkalommal esős idő miatt nehezen ment a tűzgyújtás. Látta ezt András is, akinek mi sem volt természetesebb, minthogy az előadását – bemutatása után – cafatokra tépve a parázsra dobja.

Történt egyszer, hogy a bélapátfalvi szálláson felrobbant a kazán. Akkor András ártatlan tekintettel, kezében 2 kisebb darab tűzrevalóval sétált épp a kazánház irányából, meggyőzően állítva, neki bizony semmi köze az egészhez, csak tett a tűzre egy keveset és levegőt adott neki. Évekkel később már úgy emlegette az esetet, mint „amikor berobbantottam a kazánt.” Máskor gondolataiba merülve rossz helyen szállt le a mecseknádasdi buszról, így az őt fogadóhölgykoszorú – amely igényére mindig felhívta a figyelmet – elmaradt.„…nem ott szálltam le, ahol Ambrus várt (az a Nadasch tábla utáni első megálló) így aztán a csomagtartóban felejtettem a csomagjaimat. Miután az autósok már ittak, Norbit kellett megvárni, aki még Bonyhádon járt. Összességében szerencsém volt: a pécsi buszpályaudvaron várt rám a csomagom. Ilyen az, amikor az ember gyorsjáraton utazik! Szombaton fölmentünk Óbányáról a Zengőre, az nem olyan laza, mint Pécsváradról. Közben a társaság megnézte a püspökszentlászlói arborétumban a bazsarózsákat, én szép kényelmesen továbbmentem, mert tudtam, hogy az út egy 30 fokos emelkedőbe torkollik, kb. 100 méter szintkülönbséggel, ami a Vadálló köveknél lényegesen könnyebb. Így elsőnek érintettem meg a kilátót. […] Ezek után, tekintve, hogy már a szívhalál  környékezett, kényelmesen lesétáltam az ismert úton Pécsváradra, onnan busszal a kulcsos házig, aminek az eldugott kulcsát nemtaláltam, így a szomszéd kocsmában vaddisznó pörköltet vacsoráztam, este 6-kor, ami nekem korai.” A közelmúltban vele utaztam a túra helyszínére, Dunabogdányba. A célhoz közeledve felpattant a buszon, „Hohó, megjöttünk”, majd ezzel eldőlt, egy utas ölébe esett, de nem kelt fel, hiába segédkeztem, mert körforgalom következett, mondván “majd ha elmúlik a centripetális erő, addig elvagyok, nyugalom” és feküdt tovább.

 

Nyíltan mesélt a magánéletéről, a feleségéről, mi pedig megdöbbenve, rá-rácsodálkozva hallgattuk. Egyetem alatt, évfolyamtársként ismerkedtek meg. Amellett, hogy a legszebb nőre talált közel s távol, a francia irodalom szeretete hozta őket össze. Ha Andráson múlt volna, a záróvizsgájuk napján kötnek házasodnak, “akkor már úgyis ki kell nézni valahogy, megspóroltam volna egy fésülködést”. Rendkívül tájékozott, művelt embernek ismertem, aki egyszerre testesítette meg a bolondos, hóbortos tudós és az elvarázsolt, folytonosan nosztalgiázó, dalolászó úriembert.” Ha a feleségemmel pihentünk volna a nászúton a múzeumról múzeumra loholás helyett, akkor már ott összevesztünk volna. Tudod, én nagyon rendetlen vagyok, ő meg rendszerető. Ami tökéletes párosítás lenne, ha én is szeretném a rendet. “Életét nem mindennapi események színesítették, amiket a legtermészetesebb módon, egy csipetnyi kultúrával fűszerezve adott át nekünk.” A Misina 6 éves korom nagy emléke: együtt teleltem Riesz Frigyessel: valószínűleg én vagyok az egyetlen élő matematikus, aki tegezte “Frici bácsit”. Az akkori Misina toronyba nemes egyszerűséggel bezártak, mint Szélestenyerű Fejenagyot*, és harangkötél sem volt. Végül kellő dörömbölés után kiengedtek. Az izgalmakat rumos teával vezettük le, akkor én már gyakorló alkoholfogyasztó voltam.”

“Apámat, mint frissen kinevezett “orvosvegytani professzort” […]beutalták a Kikelet Szállóba […]. A matematikusok krémje is ott sürgött forgott (Rényi, Szőkefalvi és persze Riesz), akinek ott ünnepelték a 70. szülinapját. Frici bácsitól kértem problémát, ő azzal kezdte, hogy adjam össze 1-től százig a számokat, persze ezt lemondtam: a szorzást még nem ismertem kompetencia szinten. Akkor azt adta, hogy “egy fán van 10 alma, elmegy alatta 5 gyerek ki-ki leszakít kettőt, mennyi marad? Osztani kis számokkal már tudtam, de a helyes válasz 8, mert nem ki-ki, hanem Kiki. Így éltem Pannóniában.”

Elmentünk teázni Budapesten. Soha nem felejtem el a pénztáros lány arcát, amint András pénzért kutatva előveszi a táskáját és mindent kipakol: orosz szépirodalom, szamárfüles, jegyzetelt matematika cikkek, útlevél, fogkefe, egy tucat borotvapenge, táblafilc, majd a rózsaszín óvodai ballagótarisznyából a pénz. Temérdek különc történetet tudnék még sorolni róla. •A lakásában egy betörőnek felajánlotta a leveses tálját, amire neki már semmi szüksége nemvolt, mégse menjen haza üres kézzel a jóember.• A KRESZ vizsgáján fel tudta sorolni Budapest akkori összes(!) STOP tábláját.• Egyszer egy előadásra késve érkezve ez a felirat várt a táblán: “Kórházban vagyok.” Kiderült, aznap a klinika kertjében egy padon ücsörögve tartotta az órát.• Egy konzultáció során tábla és poszter híján az aznapi Délmagyarra vezette le a tételbizonyítást.• A személyes adatok védelmében, nevek helyett kódokkal jegyezte fel a diákok beadandó dolgozatból származó pontjait, majd alkalmanként az azonosításhoz használható összes kulcsot is mellékelte mindenkinek.• A párizsi nyaralásának nagy szívfájdalma, hogy nem ehetett osztrigát, mivel az abból származó ételmérgezést nem fedezte volna a biztosítása.• A Google profilképe Moszkvában készült róla, méghozzá úgy, hogy ő a nyaralásra nem vitt magával sem telefont, sem fényképezőgépet. Egy szimpatikus járókelőt leszólított, megkérte, hogy készítsen róla egyet, majd küldje el neki email-ben.• A 70. születésnapjára kapott egy bögrét, amin a kirándulókkal közös csapatfotó szerepel. Ezt akkora becsben tartotta, hogy kizárólag ebből ivott otthon. A későbbiekben ugyanezt kétszer  is elkészíttette, mivel “a huzat becsapta az ablakot, aminek a párkányán a 70-es kép őrződött, most restaurálódik”.

A legutolsó kirándulása előtt ezt írta: “Képzeld, 3 héten belül $3\times$ estem sima úton ugyanarra a jobbkezemre, utoljára tegnapelőtt. Az első kettőtől nem lett semmi bajom, de tegnap (megfogadva Vonnegut tanácsát)* két kézzel borotválkoztam, mára radikálisan javult a helyzet, kicsit lassabban, de jobb kézzel rendesen tudok borotválkozni, cipőt bekötni könnyebb terhet cipelni (hálózsák). A bal kezem teljesen ép, a lábaim, szívem, tüdőm a régiek. Az a tervem, hogy néhány lassabb de egyenletes ütemű kirándulóval Pécsváradon át […]fölugranék a Zengőre, ki tudja lesz-e még rá alkalmam fölmenni a Zengőre? Azon az úton a hasra esés esélye kisebb, mint éjszaka az Alföld tengersík vidékin, ahol a gödör ugyanolyan sötét, mint a nem-gödör.”

Krámli András Nekrológ URL

Krámli András: Szász Domonkos írása URL

In memoriam: Krámli András URL

Krisztin Tibor (1956-)

Forrás a képre kattintva látható.

A szegedi matematikus – többek között – késleltetett differenciálegyenletekkel foglalkozik. Ilyenek fordulnak elő például az irányítási feladatokban, a fertőzések terjedésének modellezésében, a pénzügyi folyamatok leírásában.

1975-ben érettségizett a szegedi Radnóti Gimnázium matematika-fizika tagozatán. A József Attila Tudományegyetemen 1981-ben végzett. Egyetemi doktori címet 1982-ben szerzett. A matematikai tudományok kandidátusává 1988-ban avatták a Magyar Tudományos Akadémián, dolgozatának címe: On the asymptotic behavior of solutions of functional differential equations. 200-ben tudományok doktora, dolgozata címe: Global dynamics of functional differential equations.

Curriculum vitae URL

1981-87 között a JATE Bolyai Intézetében kutató. 1987-1989 között adjunktus, 1989-2000 között docens, 2000-től egyetemi tanár. 2005-től az Alkalmazott és Numerikus Matematika Tanszék vezetője.

 

Külföldi kutató és oktatói munkái:

  • Memphis State University, TN, USA; visiting assistant professor, 1983, 5 hónap
  • University of Alberta, Edmonton, Canada; post-doctoral fellowship, Government of Canada Award, 1990-91, 8 hónap
  • University of Pau, France; research fellowship, 1995, 3 hónap
  • Universität Giessen, Germany; Humboldt Fellowship, 1996-97, 15 hónap
  • University of South Florida, Tampa, USA; visiting professor, 2001, 4 hónap
  • Universität Giessen, Germany; Humboldt Fellowship, 2002, 6 hónap
  • Universität Giessen, Germany; Humboldt Fellowship, 2011, 2 hónap
  • York University, Toronto, Canada, visiting professor (2015)
  • Acta Scientiarum Mathematicarum, 1993-
  • Differential Equations and Dynamical Systems, 1993-2018
  • Alkalmazott Matematikai Lapok (in Hungarian), 2004-
  • Journal of Mathematical Analysis and Applications, 2004—2007
  • SIAM Journal of Mathematical Analysis, 2004-2016
  • International Journal of Dynamical Systems and Differential Equations, 2007-
  • Communications in Differential and Difference Equations, 2006-
  • Journal of Qualitative Theory of Differential Equations and Applications, 2007-
  • Discrete and Continuous Dynamical Systems Series S, 2007-2010
  • Electronic Journal of Qualitative Theory of Differential Equations, Co-Editor-in-Chief, 2015-
  • Matematikai Tudományos Bizottság
  • Chair of the Selection Committee of the Hungarian National Science Foundations in Mathematics, Magyar Nemzeti Tudományos Alapítványok  válogatott bizottságának elnöke, 2004-2007
  • Magyar Tudományos Akadémia, Doktori Tanács, 2007-2013
  • SZTE Bolyai Intézet vezetője, 2011-2014
  • Magyar Tudományos Akadémia Természettudományi Kutatóközpontja, bizottságának elnöke 2014-2017
  • Szegedi Tudományegyetem Egyetemi Habilitációs Bizottság elnöke, 2015-
  • MTA TABT Szegedi Akadémiai Bizottság alelnöke, 2014-2020
  • Magyar Tudományos Akadémia Matematikai Bizottságának  alelnöke, 2017-2020. szept. 5-től a Szegedi Akadémiai Bizottság elnöke
  • Rényi Kató díj (Bolyai Társulat), 1981
  • Grünwald Géza emlékdíj, 1984
  • Magyar Arany Érdemkereszt, 2005
  • Ipolyi Arnold díj, 2007
  • Akadémiai Díj, 2009
  • Mestertanár Aranyérem, 2009
  • Magyar Tudományos Akadémia, levelező tag, 2013
  • Best JDEA Paper 2013 Prize Winner (megosztva: Ferenc A. Bartha, Ábel Garab URL
  • Szele Tibor emlékdíj, 2016 URL
  • 2016 Moore Prize for Application of Interval Analysis

Kollégáival együtt 2016-ban azért nyerte el a Reliable Computing elnevezésű nemzetközi szaklap szerkesztőbizottságától a Moore-díjat, mert – a szegedi Bánhelyi Balázzsal és Csendes Tiborral, valamint a bécsi Arnold Neumaierrel közösen – igazolták Edward Maitland Wright angol matematikus 1955-ben megfogalmazott sejtését csaknem a teljes megadott paramétertartományban arról, hogy egy viszonylag egyszerű késleltetett differenciálegyenlet megoldásai nullához tartanak.

  • Szegedért Alapítvány Szőkefalvi-Nagy Béla díja, 2017 URL
  • Széchenyi Díj, 2018
  • Magyar Tudományos Akadémia, rendes tag, 2019
  1. The unstable set of a periodic orbit for delayed positive feedback. J. Dynam. Differential Equations 28 (2016), no. 3-4, 805–855. (with G. Vas)
  2. Parabolic partial differential equations with discrete state-dependent delay: classical solutions and solution manifold. J. Differential Equations 260 (2016), no. 5, 4454–4472. (with A. Rezounenko)
  3. Global attractivity of the zero solution for Wright’s equation. SIAM J. Appl. Dyn. Syst. 13 (2014), no. 1, 537–563. (with B. Bánhelyi, T Csendes, and A. Neumaier)
  4. Local stability implies global stability for the 2-dimensional Ricker map. J. Difference Equ. Appl. 19 (2013), no. 12, 2043–2078. (with F.A. Bartha and A. Garab)
  5. Large-Amplitude Periodic Solutions for Differential Equations with Delayed Monotone Positive Feedback, J. Dynam. Differential Equations 23 (2011), 727-790. (with G.Vas)
  6. Functional differential equations with state-dependent delays: theory and applications, In: Handbook of Differential Equations, Ordinary Differential Equations, vol. 3, Editors A. Canada, P. Drabek and A. Fonda, Elsevier, 2006, pp. 435-545. (with F. Hartung, H.-O. Walther and J. Wu)
  7. Invariance and noninvariance of center manifolds of time-$t$ maps with respect to the semiflow. SIAM J. Math. Anal. 36 (2004/05), no. 3, 717-739.
  8. The two-dimensional attractor of a differential equation with state-dependent delay. J. Dynam. Differential Equations 13 (2001), no. 3, 453-522. (with O. Arino)
  9. Unique periodic orbits for delayed positive feedback and the global attractor. J. Dynam. Differential Equations 13 (2001), no. 1, 1-57. (with H.-O. Walther)
  10. Connecting orbits from synchronous periodic solutions to phase-locked periodic solutions in a delay differential system. J. Differential Equations 163 (2000), no. 1, 130–173. (with Y. Chen and J. Wu)
  11. Shape, smoothness and invariant stratification of an attracting set for delayed monotone positive feedback. Fields Institute Monographs, 11. American Mathematical Society, Providence, RI, 1999. viii+245 pp. (with H.-O. Walther and J. Wu)
  12. A necessary and sufficient condition for the asymptotic stability of the damped oscillator. J. Differential Equations 119 (1995), no. 1, 209–223. (with L. Hatvani and V. Totik)
  13. An invariance principle of Lyapunov-Razumikhin type for neutral functional-differential equations. J. Differential Equations 107 (1994), no. 2, 395–417. (with J.R. Haddock, J. Terjéki and J. Wu)
  14. On the existence of periodic solutions for linear inhomogeneous and quasilinear functional-differential equations. J. Differential Equations 97 (1992), no. 1, 1–15. (with L. Hatvani)
  15. On stability properties for one-dimensional functional-differential equations. Funkcial. Ekvac. 34 (1991), no. 2, 241–256.
  16. Stability for functional-differential equations and some variational problems. Tohoku Math. J. (2) 42 (1990), no. 3, 407–417.

Krisztin Tibor – Dinamikus Modellek a Közgazdaságban URL

Krisztin Tibor – Shape, Smoothness and Invariant Stratification of an Attracting Set for Delayed Monotone Positive Feedback URL

Krisztin Tibor: a számítógépek egyre nagyobb szerepet kapnak a matematikában URL

Újszászi Ilona riportja URL

Krisztin Tibor beszél matematikáról, sejtésekről és bizonyításokról a Kossuth Rádióban URL (nem elérhető)

Kudar János (1906-?)

Forrás a képre kattintva látható.

Kudar János nevét is hiába keressük magyar lexikonokban,(életrajzi adatait sem ismerjük) holott jelentős elméleti fizikus volt. Ami keveset tudunk róla, az Gurka Dezső és Füstöss László kutatásainak köszönhető.1 Kudar a középiskolát Budapesten, az egyetemet Szegeden végezte. Az Ábrázoló Geometria Intézet tanársegédje lett, de tanársegédként működött Ortvay professzor mellett is, a Matematikai Fizika Tanszéken matematikusi pozícióban, gyakorlatilag elméleti fizikusként. Kudar Ortvay révén jutott három éves németországi kutatási ösztöndíjhoz, ezért helyére a geometria tanszékére – tanársegédnek Lipka Istvánt nevezték ki 1926. szeptember 1-jével. Kudar Németországban és Dániában dolgozott neves fizikusok mellett (Pauli, Schrödinger, Bohr), az Amerikai Egyesült Államokban halt meg. 

Az ő nevéhez fűződik a relativisztikus Schrödinger egyenlet első levezetése. 

Amikor Kudar közölte Ortvay professzorral, hogy ösztöndíja lejárta után nem kíván hazatérni, Ortvay is kénytelen volt új munkatárs után nézni. Kürschák József műegyetemi professzor ekkor ajánlotta helyére Kalmár Lászlót. Kalmár kapva kapott az ajánlaton, bár nem hallgatta el, hogy őt igazán és elsősorban a matematika érdekli. Ortvay kifejtette, hogy ez nála előny, mivel az elméleti fizika matematikailag jól képzett szakembereket igényel. Így került 1927. szeptember 1-jével Kalmár a Matematikai Fizika Tanszék tanársegédi posztjára. Kudarnak tehát két utóda is volt a szegedi egyetemen, Lipka István és Kalmár László.

Gurka Dezső  G. Csizmás Edit: Magyarok a Bohr Intézetben, A kvantummechanika bölcsőjénél, Első rész URL

Gurka Dezső  G. Csizmás Edit: Magyarok a Bohr Intézetben, A kvantummechanika bölcsőjénél, Második rész URL

 

Kurusa Árpád (1961-)

Forrás a képre kattintva látható.

(Szeged, 1961. október 24. –) magyar matematikus, egyetemi docens. A Szegedi Tudományegyetem TTIK Bolyai Intézete Geometriai tanszékét 2000 óta vezeti. A Grünwald Géza díjat 1990-ben nyerte el.

Minden iskoláját a Szegedi Tudományegyetem intézményeiben végezte: a Ságvári Endre Gyakorló Gimnázium matematika szakos osztályából 1980-ban érettségizett, majd egy évnyi katonaság után a Szegedi Tudományegyetem matematikus szakának elvégzésével szerezte matematikus diplomáját 1986-ban. 

Az egyetem elvégzése után a Szegedi Tudományegyetem TTIK Bolyai Intézete Geometriai tanszékére került, ahol a Magyar Tudományos Akadémia TMB-ösztöndíjasaként 1990-re készítette el kandidátusi disszertációját. Az MTA Tudományos Minősítő Bizottságától 1991-ben kapta meg kandidátusi (C.Sc.) fokozatát. Magyarországon eddig mindig a Szegedi Tudományegyetem TTIK Bolyai Intézete Geometriai tanszékének munkatársa volt. Előbb tudományos segédmunkatárs, aztán munkatárs, 1991-től főmunkatárs, majd 1996-tól egyetemi docens lett. 2000-ben a tanszék vezetőjévé nevezték ki. Egyetemi állása mellett 1992-ben az MIT, 1993/4-ben a University of Erlangen-Nuremberg majd 1995-ben a University of Maryland vendégprofesszora volt.

Az Acta Scientiarum Mathematicarum című tudományos folyóiratnak 2000-től szerkesztőbizottsági tagja, 1991-ben részt vesz a Polygon Kiadó alapításában; a Polygon szakdidaktikai folyóiratnak azóta is szerkesztőbizottsági tagja, a Polygon Jegyzettár sorozatának pedig 1994-es indulása óta szerkesztője.

A geometriai analízis, azon belül az analitikus és geometriai tomográfia. Jelentős eredménye John ultrahiperbolikus egyenlete megoldásának általánosítása tetszőleges dimenzióra, valamint a különböző terek Radon transzformációi közti kapcsolatok feltérképezése

Matematika iránti érdeklődéséről, tanulmányairól és pályakezdéséről a következőket írja:

“A Ságvári általános iskolába jártam éppen akkor, amikor kísérleti matekos osztályt indítottak. Ez volt a véletlen. A matek tanárnő (Szécsi Imréné) nem csak matekot tanított nekem, hanem sokszor meg is kellett fegyelmeznie. Volt, hogy kizavart az osztályból…. mégis szerettem, ahogy szerettem a tantárgyat is…. Emlékszem, hogy lisztet kellett bevinni az órájára és kartonból ragasztottunk hengert meg kúpot és a lisztet öntögetve derítettük ki, hogy a hengerbe pont háromszor annyi liszt fér mint a kúpba. Ez volt az első értelmes találkozásom a térfogat fogalmával. Az igazság az, hogy engem akkor és még ma is szinte minden érdekel. A fizika volt a kedvencem, aztán a kémia, de a történelem is fontos volt és kenuztam is, nem annyira érdeklődésből, mint inkább a társaság kedvéért….

 A középiskolai jelentkezést a Ságvári fizika szakára adtam be, de a felvételin Pintér Lajosnéba és Hajnal Imrébe “ütköztem”, akik olyan sokáig mondták (volt az vagy fél órás rábeszélés…), hogy inkább a mat. 2-re menjek (legfőbb érvük az volt, hogy ha a matekot választom, akkor a fizikát is jobban fogom tudni), hogy végül beadtam a derekam. Így kerültem a Ságvári Mat.2-tagozatára, ahol már a legfontosabb a matek lett, de ez csak jóval később vált számomra világossá. Mindenféle versenyeken elég jól szerepeltem mind matekból (országos második volt a legjobb eredményem), mind fizikából (Budó Ágoston versenyt nyertem például) és amíg csak elmélet kellett, addig kémiából is. A matek és a fizika, pontosabban az elektronika kereszteződésében (mindenféle elektronikai cuccokat építettem otthon szétszedett régi tévék és rádiók alkatrészeiből, majd azokon túl lépve pár digitális áramkört is összehoztam) találtam a számítógépet, ami akkor elérhetetlen volt ugyan, de programozási nyelveket már lehetett tanulni, és egy Ságvári Napok alkalmával olyan dolgozatot adtam be, amelyben egy digitális áramkörökkel építhető Hanoi tornyai játék terveit írtam le. Egy másik évben meg a prímszámokról írtam egy dolgozatot…

 Egyszer egy nyári matekos olimpiai előkészítő táborban megjelent Erdős Pál. Elhívott minket (voltunk úgy 10-en) fagyizni, aztán beszélgettünk, de ő elaludt. Matekra fordult a szó, és mi nem nagyon tudtunk eldönteni valamit, de Erdős Pál egyszer csak felébredt, és mintha nem is aludt volna, közölte a kézenfekvő megoldást. Mind le voltunk nyűgözve. Soha azelőtt és azután sem találkoztam Erdőssel.

 Az egyetem-választás aközt dőlt el, hogy CPU-építést (ez a számítógépek központi egysége, egy digitális áramkör általában egyetlen szilikon lapon) vagy matekot akarok tanulni.

Nem volt könnyű döntés, de az utóbbi mellett döntöttem, az elektronikát meg félre tettem a hobbi szintjére.

 Angol órán megismertem a későbbi feleségem. Ma már egy fiunk és egy lányunk van.

 Azóta is szeretem a számítógépeket, az hardver és szoftver szintjén is (valamelyest értek is hozzá!).

Imádok túrázni, de kevés alkalom adódik rá.

 Az egészen biztosan különcé tesz a matekosok között, hogy az üzlet is érdekel, és egyik alapítója voltam az ország egyik első internetszolgáltatójának (üzlet és számítástechnika egyszerre: dupla öröm! 🙂 ), a TiszaneTnek, amit aztán eladásáig vezettem.

Középiskolásoknak talán a következő oldalt ajánlom, mert az a saját felfedezésemről (fentebb jeleztem, hogy Ságvári Napra adtam be egy munkát a prímszámokról) szól, amiről később aztán kiderült, hogy már mások is felfedezték, de egyelőre nem bizonyított, hogy igaz lenne…. URL

Kurusa Árpád honlapján a geometria iránt érdeklődők számos érdekességet találhatnak URL

Kurusa Árpád kedves tanárjairól URL

Kurusa Árpád Wikipédia URL

Kurusa Árpád Weboldala URL

Házi kézírás közvetítők URL

Újszászi Ilona: Krong vagy Gömb? URL

Leindler László (1935-2020)

Forrás a képre kattintva látható.

Leindler László Kecskeméten született 1935. október 1-én. Általános és középiskolai tanulmányait szülővárosában, egyetemi tanulmányait 1954-től a Szegedi Tudományegyetem matematika–fizika szakán végezte. 1958-ban kapott tanári diplomáját követően egy évig a veszprémi Vegyipari Technikum matematikatanára volt, majd 1959-ben aspiráns lett Tandori Károly és Alexits György vezetésével. 1962-ben szerezte meg egyetemi doktori címét Sub –Auspiciis Rei Publicae kitüntetéssel. Disszertációjának címe: Studies on convergence and summability concerning general orthogonal series. Témavezetői Tandori Károly és Alexits György voltak. ugyanebben az évben védte meg kandidátusi disszertációját. 1966-ban lett az MTA doktora, értekezésének címe “Ortogonális függvénysorok konvergenciájára és szummálhatóságára vonatkozó vizsgálatok”.

1962-ben a József Attila Tudományegyetem adjunktusa, később docense lett; 1968-tól ugyanott egyetemi tanár. 1977-ben kinevezték a Halmazelméleti és Matematikai Logikai tanszék vezetőjének. 1983-ban került az Analízis Tanszékre tanszékvezetőként, melyet 1998-ig vezetett. Az 1967-1971 periódusban a Természettudományi Kar dékánhelyettese, 1972 és 1975 között pedig dékánja volt. 1975-ben, 1984-ben és 1987-ben az egyetem rektorhelyettesévé választották 3-3 éves időtartamokra. 1999-ben Széchenyi professzori ösztöndíjat kapott. 2005-ben ment nyugdíjba emeritus professzori címmel.

1973-ban megválasztották a Magyar Tudományos Akadémia levelező, 1982-ben pedig rendes tagjává. 1976 és 1990 között az MTA Matematikai és Fizikai Tudományos Osztálya elnökhelyetteseként, 1996-tól 2002-ig pedig a Szegedi Akadémiai Bizottság alelnökeként dolgozott. 1982 és 1992 között az Acta Scientiarum Mathematicarum folyóirat főszerkesztője. Emellett az Acta Mathematica, az Analysis Mathematica és a Periodica Mathematica folyóiratok szerkesztőbizottságának is tagja volt.

Számos külföldi egyetem vendégprofesszora volt: Giesseni Egyetem (1977, 1980), Edmontoni Egyetem (1974, 1983, 1989, 1990), Torontói Egyetem (1993). Ezen kívül vendégkutató volt Torontóban (1966–1967) és Moszkvában (1968–1969).

Tudományos tevékenysége a klasszikus analízis területére esik, elsősorban a Fourier- és ortogonális sorok elméletére, de jelentős eredményeket ért el függvényterekkel, sorozatok osztályaival, beágyazási tételekkel  és egyenlőtlenségekkel kapcsolatban is.  Első dolgozatait  ortogonális sorok konvergenciájáról és szummációjáról írta. Figyelme hamarosan az ún. erős szummáció és approximáció felé fordult, ahol korábbi sporadikus eredmények az ő munkássága nyomán álltak össze egy egységes elméletté. E témában írt “Strong approximation by Fourier series” című 1985-ös monográfiáját a mai napig a terület alapműveként tartják számon. Későbbi eredményei közül megemlítendők a máig legáltalánosabb Hardy-Littlewood-típusú egyenlőtlenségek, az ún. inverz Hölder-egyenlőtlenségek, pontos beágyazási tételek különböző függvényosztályok között illetve a munkássága vége felé sokat vizsgált tartalmazási relációk különböző együtthatófeltételek mellett. 254 dolgozatára sok száz hivatkozást kapott a világ minden részéről. Emellett öt egyetemi jegyzet szerzője illetve társszerzője, ezekből matematikus és matematika tanár szakos hallgatók generációi sajátították el a matematikai analízis alapjait.

Rendkívül szerény egyéniség volt, saját, gyakran szemléletformálóan átütő eredményeit legtöbbször “apróságnak”, “kis javításnak” nevezte. Életében a sport mindig fontos szerepet játszott: a futball iránti szeretete fiatalkorában majdnem eltérítette az akadémiai életpályától. Később rendszeresen teniszezett – szerénységének megfelelően mindig az Erzsébet-ligeti leghátsó pályán.

  • Grünwald Géza-díj (1961)
  • Szele Tibor-emlékérem (1984)
  • Széchenyi-díj (megosztva) (1992) – A matematikai analízis témakörén belül elsősorban a klasszikus Fourier-sorok konvergencia- és összegzési kérdéseinek kutatásában elért, nemzetközileg is elismert kiemelkedő eredményeiért. Megosztott díj dr. Tandori Károllyal.
  • Klebelsberg Kunó-díj (2002)
  • Szőkefalvi-Nagy Béla-érem (2002)
  • SZAB-emlékplakett (2003)
  • a Szegedi Tudományegyetem díszdoktora (2003)
  • A Magyar Köztársasági Érdemrend középkeresztje (2004)
  • Generalization on Inequalities of Hardy and Littlewood (1970)
  • Analízis 1.; Egyetem, Bolyai Intézet, Szeged, 1972
  • Analízis 2.; Egyetem, Bolyai Intézet, 1973
  • Vizsgálatok a Fourier-analízis köréből (1974)
  • Analízis I-II. (Schipp Ferenccel, Budapest, 1976)
  • Strong Approximation by Fourier Series (Budapest, 1985) ISBN 963-05-4044-4
  • Ortogonális sorok szummálhatósága. Akadémiai székfoglaló. 1983. április 13.; Akadémiai, Bp., 1985 (Értekezések, emlékezések)
  • Some Inequalities Pertaining to Bennett’s Results (1993)
  • Improvements of Some Theorem of Mulholland Concerning Dirichlet Series (1993)
  • A funkcionálanalízis elemei; JATEPress, Szeged, 1995
  • Analízis (1995)

Tanárképzésről szóló írásai:

  • Leindler László: “Nagy felelősség hárul minden pedagógusra, mind az általános és a középisokákban, mind az egyetemen” = Magyar tudomány 1973:10. sz. 665-668. p.
  • Leindler László: “Veréb marad-e, vagy énekes madár lesz? Jó utat választunk-e? = Magyar tudomány 2007:8. sz. 1045-1046. p.

Leindler László:„Veréb marad-e, vagy énekes madár lesz?” (Jó utat választunk-e?) URL

Leindler László matematikus URL

Hajdú Péter riportja: “Sosem adtam potyán a jegyeket”  = Egyetem: a szegedi felsőoktatás információs háttérmagazinja. 7. évf, 2005. 5. szám URL

Veres Károly riportja az “Arcok a TTK-ról” rovatban = NewTon(e) : A József Attila Tudományegyetem TTK Hallgatói Önkormányzatának lapja. 2. évf. 1992. 7. szám.3-4. p.

Film: Akadémikusok nyakkendő nélkül URL

Elhunyt Leindler László matematikus, az MTA rendes tagja URL

Lipka István (1899-1990)

Forrás a képre kattintva látható.

Lipka István, teljes nevén Lipka István Károly (Újpest, 1899. május 9. – Budapest, 1990. szeptember 24.) mérnök, matematikus, egyetemi tanár, a műszaki tudományok doktora (1976).

Lipka Zoltán hajógyári mérnök és May Aranka fiaként született, római katolikus vallású. 1917-ben tett érettségi vizsgát, majd beiratkozott a Budapesti Tudományegyetem Bölcsészettudományi Karára, ahol matematika-fizika szakon tanult, mindemellett pedig a Műegyetem hallgatója is volt. 1923-ban matematikából, elméleti és kísérleti fizikából tett doktorátust, és megszerezte középiskolai tanári oklevelét is. 1923-tól három éven át Várpalotán tanított, majd 1926-ban a Szegedi Tudományegyetem geometriai tanszékén lett tanársegéd, 1929-ben ösztöndíjasként Hamburgban tanult. 1933-ban lett egyetemi magántanár, 1942-től pedig intézeti tanár a geometriai tanszéken, majd 1946-ban nyugdíjazták. Két év múlva statisztikusként a Csepel Műveknél kezdett dolgozni, később a szerszámgépgyárban gyártmánytervezőként működött. Fogaskerekekkel kapcsolatos tanulmányait a Magyar Tudományos Akadémia is támogatta. 1954-ben a Szerszámgép Fejlesztési Intézetbe helyezték át, Halásztelekre. Több mint 30 nemzetközileg is elismert dolgozatot publikált matematika tárgykörben, 42-t műszaki gépészetiben. 1990-ben hunyt el Budapesten.

  • Magyar életrajzi lexikon II. (L–Z). Főszerk. Kenyeres Ágnes. Budapest: Akadémiai. 1969.
  • Lipka István. Magyar Életrajzi Index. Petőfi Irodalmi Múzeum. Hozzáférés ideje: 2016. március 20.
  • Magyar tudományos akadémiai almanach az . . . évre. Bp., Magyar Tudományos Akadémia, 1861-1918, 1921, 1924-1943. 1973, 1986, 1991, 1997, 2001.
  • Révai Új Lexikona. Főszerk. Kollega Tarsoly István. Szekszárd, Babits, 1996-.
  • Szegedi Tanárképző Főiskola 1873-1998. Történet. Almanach. Szerk. Apróné Laczó Katalin, Pitrik József. Szeged, Juhász Gyula Felsőoktatási Központ, 1998.
  • Természettudományos és műszaki ki kicsoda? Szerk. Szluka Emil, Schneider László. Bp., Országos Műszaki Információs Központ és Könyvtár, 1988.
  • Újpest lexikon. Szerk. biz. elnöke Sipos Lajos, főszerk. Hirmann László. Újpest, Újpest Önkormányzata-Kossuth Kiadó, 2002.
  • Új magyar életrajzi lexikon. Főszerk. Markó László. Bp., Magyar Könyvklub

Lovász László (1948-)

Forrás a képre kattintva látható.

Lovász László (Budapest, 1948. március 9.) Széchenyi-nagydíjas, Bolyai-nagydíjas, Bolyai János alkotói díjas, Wolf- és Abel-díjas magyar matematikus, egyetemi tanár, a Magyar Tudományos Akadémia (és az amerikai National Academy of Science) rendes tagja. A számítógép-tudomány világhírű kutatója. 2006 és 2011 között az Eötvös Loránd Tudományegyetem Matematikai Intézetének igazgatója. 2014. május 6. – 2020. július 7. között a Magyar Tudományos Akadémia elnöke.

 

1962-től 1966-ig a budapesti Fazekas Mihály Fővárosi Gyakorló Gimnázium speciális matematika tagozatára járt. Három egymást követő évben lett aranyérmes a Matematikai Diákolimpián (1964, 1965, 1966). Osztályfőnöke Komlós Gyula, matematikatanára Rábai Imre volt. 1966-ban kezdte meg egyetemi tanulmányait az Eötvös Loránd Tudományegyetem (ELTE) matematikus szakán. 1971-ben szerezte diplomáját.

Diplomájának megszerzése után 1975-ig tudományos főmunkatársként dolgozott az ELTE geometria tanszékén. 1975 és 1982 között a József Attila Tudományegyetem geometria tanszékét vezette docensként. 1978-ban megkapta egyetemi tanári kinevezését. 1982-ben visszatért az ELTE-re, majd egy évvel később a Számítógéptudományi Tanszék vezetője lett, szintén egyetemi tanári beosztásban. 2006-tól 2008-ig az ELTE Matematikai Intézetének igazgatója volt. 1987-től a Princetoni Egyetem, illetve 1993 és 1999 között a Yale Egyetem félállású egyetemi tanára. 1972–1973-ban a Vanderbilt Egyetem, 1984–1985-ben pedig a Bonni Egyetem vendégprofesszora volt.

1970-ben védte meg a matematikai tudományok kandidátusi, 1977-ben akadémiai doktori értekezését. Az MTA Matematikai, illetve az Operációkutatási Bizottságának tagja lett. 1979-ben megválasztották a Magyar Tudományos Akadémia levelező, 1985-ben rendes tagjává. 2008-ban az MTA elnökségi tagjává is megválasztották. 1987 és 1994 között a Nemzetközi Matematikai Unió (IMU) Végrehajtó Bizottságának választott tagja volt. 1981-ben a párizsi Európai Tudományos és Művészeti Akadémia, 1991-ben a londoni Európai Akadémia, 2007-ben a Svéd Királyi Akadémia is felvette tagjai sorába.

1981-ben Erdős Pállal és Babai Lászlóval létrehozta a Combinatorica című folyóiratot. 1985-ben Babai Lászlóval létrehozta a Budapest Semesters in Mathematicsot, és a bonni egyetem John von Neumann-professzorává nevezte ki. 1999 és 2006 között a Microsoft tudományos kutatója volt. 2004-től 2006-ig az Abel-díj öttagú bírálóbizottságának tagjaként is működött. 2007-től a Nemzetközi Matematikai Unió (IMU) Végrehajtó Bizottságának elnöke. Ez a megbízatása 2010-ig szólt.

Két alkalommal a Mindentudás Egyeteme előadója volt.

Elsősorban kombinatorikával és számítógéptudománnyal foglalkozik. Számos eredménye közül kiemelkedik a gyenge perfektgráf-sejtés igazolása, a Kneser-gráfokra vonatkozó sejtés bizonyítása.

Szegeden a Geometria tanszéket (hosszabb szünet után) 1975-ben töltötték be, amikor az intézet az akkor feltűnt kiemelkedő tehetségű fiatal budapesti matematikust, Lovász Lászlót hívta meg a tanszékre. Lovász bemutatkozó előadása méltó volt kiváló elődjéhez és önmagához. A nagy Leonhard Euler a XVIII. század derekán vetett fel egy, zárt térgörbék síkra való vetületének bizonyos kombinatorikai tulajdonságára vonatkozó problémát, amelynek megoldásában először Szőkefalvi-Nagy Gyula ért el számottevő előrehaladást, Lovász pedig első szegedi előadásában ennek a problémának a teljes megoldását mutatta be.

A geometriai hipergráf fogalmának meghatározása lehetővé tette az alfa-kritikus gráfok elméletének kimunkálását és kiépítését, valamint a Shannon-féle ötszögprobléma megoldását. Nevéhez fűződik a Lovász-féle lokális lemma, a Lovász-féle bázisredukciós algoritmus: a Lenstra–Lenstra–Lovász (LLL)-algoritmus, valamint a konvex testek és rácsok algoritmikus elméletének kidolgozása.

A 2000-es évek elejétől a kombinatorikus optimalizáció területén ért el kiemelkedő eredményeket. Több mint kétszázötven tudományos publikáció és kilenc könyv szerzője vagy társszerzője.

  • Grünwald Géza-díj (1969)
  • Pólya-díj (1979)
  • Best Information Theory Paper Award (IEEE, 1981)
  • Fulkerson-díj (1982)
  • Állami Díj (1985) – a kombinatorikus optimalizáció, a gráfelmélet és a számítógép-tudomány terén elért nemzetközi jelentőségű eredményeiért, iskolateremtő tevékenységéért.
  • Szele Tibor-emlékérem (1991)
  • A Magyar Köztársasági Érdemrend középkeresztje (1998)
  • Wolf-díj (1999)
  • Knuth-díj (1999)
  • a József Attila Tudományegyetem díszdoktora (1999)
  • Corvin-lánc (2001)
  • Gödel-díj (2001)
  • a Budapesti Műszaki és Gazdaságtudományi Egyetem díszdoktora (2002)
  • a Calgary Egyetem díszdoktora (2006)
  • Neumann János elméleti díj (2006)
  • Bolyai János alkotói díj (2007)
  • Széchenyi-nagydíj (2008)
  • Bolyai-nagydíj (2008)
  • Kiotó-díj (2010)
  • Fulkerson-díj (2012)
  • Neumann János-díj professzori oklevél és plakett (2017)
  • Szőkefalvi-Nagy Béla-érem (2018)
  • Budapest Hazám-díj (2020)
  • Abel-díj (2021)

Az első Bolyai Nagydíjas: Lovász László, és székfoglalója a BME OMIKK-ban(Tudományos és Műszaki Tájékoztatás, 55. évfolyam (2008) 11-12. szám. Letöltve 2014. május 11.) URL

ELTE hírlevél. Hozzáférés: 2012-05-18. URL

Lovász László az MTA új elnöke. Origo. (Hozzáférés: 2014. május 6) URL

A BME „Neumann János” professzori címét adományozták Lovász Lászlónak. Magyar Tudományos Akadémia, 2017. május 29.  URL

Nekik csak Laci – Kiváló matematikusok Budapesten, Lovász László tiszteletére URL

Lovász László Wikipédia URL

Abel-díjat kapott Lovász László URL

A matematikusok Nobel-díjaként jegyzett Abel-díjat kapta Lovász László URL

Lovász László megtudja, hogy Abel-díjat kapott – MEGLEPETÉS!!! URL

Az első számítógépemet felértékelték a vámon a lakásunk árára URL

Makay Géza (1968-)

Forrás a képre kattintva látható.

egyetemi docens, Analízis Tanszék

1991 óta egyetemi oktató/kutató a Szegedi Tudományegyetem Bolyai Intézetében, az, Analízis Tanszéken. 1991-től tanársegéd, 1995*-től adjunktus, 1997-től docens. Oktatás: Analízis és differenciálegyenletek témájú tárgyak matematikus és tanár szakos hallgatóknak. Kutatás: Differenciálegyenletek kvalitatív elmélete, diszkrét matematikai problémák, számítógép alkalmazása matematikai problémák megoldásában. Kitüntetései: 1992: Rényi Kató díj, 1993: Grünwald Géza díj, 2001: Erdős Pál díj.

Mivel szüleim is matematikával kapcsolatos végzettségűek, nem csoda, hogy én is ebbe az irányba indultam el. Mindig jó matematika tanáraim voltak, általános iskolai (Mező Imre, ma Tiszaparti Általános Iskola) szakkörbe és versenyekre is jártam. Battancs Ferenc és Kothencz Jánosné tanítottak. De legnagyobb hatással kétségtelenül Pintér Lajos volt rám, akihez nyolcadikosként kezdtem járni a középiskolás szakkörbe. Mindig érdekes példákat hozott, hagyta, hogy gondolkozzunk akár rossz irányba is, hiszen akkor legalább az kiderült, hogy úgy nem megy a megoldás. Egy alkalommal ketten voltunk a szakkörön (a többi tanuló valamiért nem jött el), de így is megtartotta a szakkört. Ekkor adta fel azt a példát, hogy ha A egy pozitív irracionális szám, akkor az [n*(1+A)] és az [n*(1+1/A)] sorozatok ([] az egészrész függvény) kiadják az összes pozitív egész számot, és mindegyiket csak egyszer. Ezzel kapcsolatban hagyott engem “elkalandozni”, mert érdekelt, hogy egy sorozatról hogyan lehet könnyen megállapítani, hogy [n*B] alakú. Ott megfogalmaztam egy sejtést, amit a következő szakkörre be is láttam, de jól leírni csak Pintér Lajos 80-adik születésnapjára sikerült, amikor meg is jelent egy cikkben (Polygon XX. évf. 1. szám, 2011). Szintén Ő kérdezte meg tőlem a felvételi elbeszélgetésen, hogy mi a matematika, mivel akarok foglalkozni. Nem tudtam rá válaszolni, ma sem tudok pontos választ adni, de csinálom… 🙂 . Ha mégis valamit mondanom kell, akkor azt mondom, hogy a matematika alapvetően modellezés már általános iskola alsó tagozattól kezdve: 1 alma meg 1 alma az 2 alma, de az már egy általánosítás, absztrakció, modellezés, ha azt mondom, hogy 1+1=2, hiszen az elvonatkoztat a konkrét dologtól, más szóval ez bármilyen dologra igaz lesz. És ez felső tagozaton, középiskolában, egyetemen ugyanígy megy, csak persze egyre komplexebb dolgokkal.

Középiskolás (Ságvári Endre, ma SZTE Gyakorló Gimnázium) korom óta programozom. A számítógépekkel való ismerkedést nyilván én is játékokkal kezdtem: a középiskolában ABC80, HT-1080Z és Commodore 64 gépek voltak. Az első számítógépem egy Primo A-64-es volt, amit Basic-ben és Assembly-ben lehetett programozni. Mivel nem sok játék volt rá, és Assembler sem, ezért a HT-1080Z-ről (ami processzor szinten kompatibilis volt a Primo-val) átvettem onnan az Assemblert, ehhez el kellett tudnom olvasni a HT-1080Z kazettáját is. Ez később “elfajult” nálam, és szinte minden hozzáférhető számítógéptípus kazettáját tudtam olvasni, így tudtam adatokat és (néha) programokat átvenni azokról (ami ma, az Internet világában kicsit nevetségesnek tűnhet… 🙂 ). Mivel más gépeken volt “turbó” (hogy tömörebben tudtak írni a kazettára, mint gyári beállítással), ezért nekem is “muszáj” volt írnom egyet Primo-ra, ami 4-szer gyorsabb volt a gyárinál, belefért a képernyőmemória elhelyezkedése miatt sosem használt 2 kilobyte-os memóriarészbe, de csak egyfajta magnóval működött. És persze írtam Primo-ra játékokat is: mai szemmel nézve elég egyszerű kis játékok voltak, de jó szórakozás volt. Akkor volt a bűvös kocka nagy újdonság, úgyhogy írtam Basic-ben egy programot, ami kiforgatta a bűvös kockát, aztán egy Basic-ről Pascal-ra fordító programot is, hogy azt a Volán “nagy gépén” is tudjam futtatni.

Egyetem óta programozom komolyabb dolgokat. Kiderült számomra (néhány programozó szakdolgozó kapcsán), hogy a programozói végzettség nem elegendő ahhoz, hogy valaki jó programozó legyen, ahhoz logikus, modellező gondolkodás kell, amit leginkább a matematika ad meg. Nagyon sokféle programot írtam már: adatbázisokat írtam mindenféle nyilvántartó és vezérlő programokhoz; matematikai problémákra írtam programokat, amelyekkel sejtést lehet szerezni az adott probléma megoldásáról; szimulációs programokat írtam sokféle gyakorlati problémára, és még sorolhatnám. Néhány érdekesebb példa:

  – Nagy üvegtáblákból a megrendeléseknek megfelelő kisebb táblák kivágásának a vágógép korlátait figyelembe vevő optimalizálása

  – Orvosi képfeldolgozás, szervek szegmentálása CT képeken

  – Sudoku példák generálása, logikai lépésekkel való megoldása URL

  – Fém-üveg felületek háromszögekre, négyszögekre és hatszögekre bontása

  – Általános iskolás tanulók számítógép alapú tesztelése, egyetemi bemeneti mérés, eredmények elemzése

  – Közlekedési lámpák vezérlése, online ellenőrzésére szolgáló szoftver

  – Kézi és automata raktár szoftver

  – Raktár nyilvántartás, gyártás ütemezés, beléptető rendszer, automata targonca vezérlő szoftver

  – A Bolyai épület beléptető rendszer hardware-es átvétele, biztonságtechnikáinak (beléptető, riasztó és kamera) egy rendszerbe foglalása

  – Videokártyára írt 2560 szálon párhuzamosan futó program, amivel a koronavírus terjedését szimulálják a kormány által megbízott szegedi kollégák (ezzel a korábbi kb. 6 órás futási időt 7 másodpercre csökkentettem)

Ezek többségénél nem maga a kódolás volt a nehéz, hanem kitalálni a megfelelő eljárást, algoritmust, ami alapján a programnak működnie kell és ehhez egy modellező, matematikus gondolkodásmód kell. Arra büszke vagyok, hogy az ügyfeleim egymásnak adják a nevemet, nem kell reklámra költenem, és még sosem fordult elő, hogy egy ügyfelem azt mondta volna, hogy nem azt kapta, amire gondolt. Gyakran kell olyasmire is gondolni, amire az ügyfél nem gondolt, hogy a későbbi problémákat elkerüljük, vagy olyasmit is megvalósítani, amire majd úgyis szükségük lesz. Ehhez viszont “rendesen bele kell mászni” a projektbe, meg kell érteni, hogy hogyan működnek a dolgok, így én eléggé jól képzett “orvos”, “épület tervező”, “raktáros” és “biztonsági szakértő” is lettem a fenti projektek következményeképpen… 🙂 .

Szeretek kerékpározni, sétálni, túrázni. Részt veszek (kevésbé vírusos időkben 🙂 ) a Bolyai Intézet által szervezett kirándulásokon, hétvégi főzőcskézéseken, a matematikus hallgatók kirándulásain. Néha még főzésre is rá tudnak venni, de csak a specialitásomat, a sütőben sült csirkecombot szoktam csinálni, bár előfordult már, hogy négy serpenyővel sütöttem a palacsintát… 🙂 .  A Bolyai Intézetben a társasjáték “szeminárium” oszlopos tagja és szervezője vagyok, és persze nem tagadhatom meg magamat ott sem: némelyik játékot megpróbálom elemezni…

Előadás videója:

Egyetemi Tavasz 2012 – Dr. Makay Géza: Sudoku előadás és vetélkedő URL

/Saját írása/

Maróti Miklós (1973-)

Forrás a képre kattintva látható.

Szegeden született, 1973. jan. 17-én. A Radnóti Gimnázium matematika szakán érettségizett, az egyetemet 1996-ban végezte el. A PhD-t a nashville-i Vanderbilt University-n szerezte meg, 2002-ben. 2007-ben a Szegedi Tudományegyetemen is PhD fokozatot szerzett.

Az Algebra és Számelmélet tanszék docense, jelenleg vezetője.

Univerzális algebra, hálóelmélet, komplexitás elmélet, logika, kombinatorika, beágyazott rendszerek, szenzorhálózatok,  rádió alapú helymeghatározás, szoftver alapú rádió, mesterséges intelligencia (a DARPA SC2 versenyén második helyet elért MarmotE csapat technikai vezetője)

Új docensünk: dr. Maróti Miklós

 Szeretném bemutatni az Alma Material olvasóinak dr. Maróti Miklóst, az Algebra és Számelmélet Tanszék új docensét. Honlapjáról verseny-eredményeit, rangos díjait, cikkeit elolvashatjuk, tudományos eredményeiről is tájékozódhatunk. Rengeteg van mindegyikből, itt most nincs hely felsorolni az összes lényegeset, de mindenképpen érdemes egy pillantást vetni a szakmai önéletrajzra a honlap „Vitae” menüpontjában. Sokak véleménye szerint kiemelkedő képességű matematikusról van szó. Nekem hatalmas munkabírása is feltűnt, de az is, mindig és mindenkivel barátságos tud lenni; mindenre kíváncsi, minden újdonság érdekli, akkor is, ha éppen most érkezett egy több mint 24 órás repülőútról, a Föld másik feléről. Első éves hallgató kora óta ismerem, de közelebbről csak azóta, hogy szobatársak vagyunk a Bolyai Intézetben. Most azonban ez az interjú az interneten keresztül készül, ugyanis Miklós éppen Prágában tartózkodik, én pedig Szegeden. 

-Hogyan kerültél Prágába?

 -2006-ban az AAA 72 konferencián Budapesten megkeresett Jiri Tuma, a prágai Károly Egyetem Algebra Tanszékének vezetője, hogy nincs-e kedvem egy félévet Prágában tölteni, és ott kutatni, oktatni. Nagyon örültem a meghívásnak, mert eddig “csak” PhD-s témavezetım, Ralph McKenzie hívott meg hosszabb időre. 

-Ott mivel foglalkozol?

 -Angolul tartok speciálkollégiumot a : “Special Course on the Constraint Satisfaction Problem” címmel, ami 4 óra előadást és 2 óra gyakorlatot foglal magában. Ezen kívül szemináriumokra járok, próbálom befejezni az elmaradt cikkeimet, és sok új problémával is foglalkozom.

 -Hogyan telnek napjaid?

 -Sajnos nagyon gyorsan telik az idő. Nagyon jó, hogy itt sokkal kevesebb olyan feladattal kell foglalkoznom, ami kizökkentene a kutatásból.

-Haladjunk időrendi sorrendben. Mikor derült ki, hogy érdemes matematikával foglalkoznod? 

-Elég jó voltam matematikából általános iskolában, de semmi különöset nem éreztem, ének-zene tagozatos voltam, és hegedülni tanultam. Nyolcadikos koromban volt egy helyi matematikaverseny az iskolában, ahol jobban szerepeltem, mint sokak, akik jártak matematika szakkörre. Valószínűleg csak ezért jelentkeztem a Radnóti Gimnáziumba, és nem a konzervatóriumba

.-Gyermekkorodban kiktől tanultál legtöbbet?

-Legtöbbet gimnáziumi tanáromtól, Mike Jánostól, illetve a Bolyai Intézet által szervezett matematikai szakkörön Pintér Lajostól tanultam. A matematika iránti érdeklődésemet viszont a sok versenyen való részvétel hozta meg igazán.

-Családod tagjai mivel foglalkoznak? 

-Mindenki biológus (szüleim és bátyám is), éppen ezért még véletlenül sem akartam biológus lenni. -Miért éppen az algebrát választottad?

-Ebben meghatározó volt Szendrei Ágnes személye és oktatási stílusa. Nagyon érdekesnek találtam első éves koromban az axiomatikus megközelítést egy olyan tárgynál, amiről addig semmit se tudtam. -A matematika mely részei érdekelnek az algebrán kívül jelen pillanatban? 

-Logika, halmazelmélet, algoritmusok (számítástechnika), és mindenféle diszkrét matematika érdekel a leginkább.

-Miért éppen a Vanderbilt University-n készítetted a PhD-det? 

-Mert az univerzális algebra szerintem legnagyobb alakjától, Ralph McKenzie-tıl tanulhattam. 

-Mi az, ami tetszett ott, és örülnél, ha nálunk is megvalósulna? Mik a hasonlóságok, és a mik a lényeges különbségek egy amerikai és egy magyar egyetem között? 

-Nagyon jó volt, hogy mindig volt néhány vendégprofesszor az egyetemen, aki algebrával akart foglalkozni. A problémák jöttek és mentek, és nagyon hamar rájött az ember, hogy ha nem foglalkozik valamivel 100%-osan, akkor semmi esélye felvenni a versenyt a többiekkel. Nagyon szeretném, ha Szeged hasonló kutatói központ lehetne, és nem csak algebrából hanem más témákban is. Jó lenne például, ha néhány tárgyat angolul oktatnánk, mint például itt Prágában. Itt mindenki természetesnek veszi (másod és harmadévesek is), hogy egy speciálkollégiumot angolul tartanak. Szerintem, átlagban a szegedi diákok színvonala még mindig magasabb, mint a vanderbiltes diákoké. A nagy különbség ott van, hogy egy amerikai diák (aki 20-30 ezer dollár éves tandíjat fizet) mindent megtesz azért, hogy jó jegyet szerezzen (tanulással vagy könyörgéssel), és meg sem próbálkozik azzal, hogy csaljon a teszteken. Kint a 3-as egyáltalán nem jó jegy, mert a rossz átlaguk miatt sokan vesztik el a támogatásukat, vagy nem nyernek felvételt az orvosi egyetemre (ott ugyanis az orvosi egyetem előtt el kell végezni egy másik egyetemet, vagy főiskolát). Az oktatóknál is nagyon nagy a különbség. Akinek egy jó egyetemen jó állása van, annak egyáltalán nem kell azzal foglalkozni, hogy miből tartsa fent a családját, vagy vegye meg a következő kocsiját. Ott a kutató ha jó, akkor teljes mértékben a kutatásnak szentelheti az életét, és bőven marad még ideje, hogy utazzon, és a hobbijával foglalkozzon.

 -Gyakran meghívott előadóként szerepelsz nemzetközi konferenciákon (például: http://www.math.vanderbilt.edu/~oal2007/invitedspeakers.php), illetve fő szervezője voltál idén nyáron a szegedi Algorithmic Complexity and Universal Algebra konferenciának. (A konferencia honlapja: http://www.math.u-szeged.hu/confer/algebra/.) A nemzetközi tudományos konferenciákról azonban egy átlagember csak keveset hallhat. Miért fontosak a nemzetközi konferenciák szerinted a matematika szempontjából? Miért szép, és miért nehéz egy konferencia megszervezése? 

-Nekem nagyon meghatározó, hogy részt vegyek konferenciákon (a lista: http://www.math.u-szeged.hu/~mmaroti/publications.html lap végefelé olvasható). Nem azért, mert minden előadás annyira érdekelne, vagy hogy annyi emberrel tartanám a kapcsolatot. De néhány előadás meghatározó, mert olyan dologra vetít fényt, amirıl vagy sosem hallottam még, vagy mindig másképpen gondolkoztam róla. Azért a 4-5 előadásért érdemes konferenciákra menni, de sajnos a legtöbb esetben az ember nem tudja előre, hogy melyik az a néhány előadás, ami leginkább felkelti az érdeklődését. A matematika sokkal gyorsabban fejlődik ma szerintem, mint 100 évvel ezelőtt. Csupán a legnehezebb problémák esetében lehet csak levelezésre és publikációkra hagyatkozni, de még ott is meghatározó a személyes kontaktus. Két ember nem 200 %-os munkát képes végezni, hanem 300 %-osat, de sajnos ez az arány rohamosan 100 % alá csökken, ahogy az emberek száma nő. Bevallom, a konferencia szervezésében szépséget én nem találtam, azonban most már jobban átérzem azoknak kollégáknak a nélkülözhetetlen munkáját, akik lehetővé teszik a matematikusok számára szintén nélkülözhetetlen konferenciákat. 

-Újszerű kezdeményezés az úgynevezett pizza-szeminárium, amelyet dr. Zádori László kollegánkkal együtt vezettek. A szeminárium nagyon népszerű, és sikerült fiatalokat is bevonni a munkába. Mik a célkitűőzéseid, tapasztalataid a szemináriummal kapcsolatban, hogyan folytatjátok, ha hazajössz? -Sajnos egyáltalán nem olyan népszerű, mint amilyen lenne például Amerikában. Ha kint egy ilyen szemináriumot meghirdetnék, akkor annyian jönnének, amennyien beférnek a terembe, és a megrendelt pizzát meg tudnák enni. Azok is eljönnek, akik az elején még egy kukkot se értenek az előadásból. Ennek ellenére nagyon örülök, hogy van egy lelkes tábor, aki rendszeresen jár a szegedi pizza-szemináriumra. Szeretném, ha más témákban (nem csak algebrából) is lennének előadások. Itt az a lényeg, hogy mindig mindent be kell bizonyítani. Ha a diák valamit nem ért meg, akkor olyan részletességgel el kell mondani, hogy az számára is érthetőlegyen. Természetesen szeretném, ha a szeminárium tovább folytatódna.

-Kérlek, mutasd be a Hozzád legközelebb álló matematikusokat! Miben sikerült együttműködni velük, hogyan tartjátok a kapcsolatot, mi a munkamódszeretek? Milyen eredményeket sikerült elérnetek, miben segítitek egymást? 

-Ez nagyon nehéz kérdés. Három matematikus van hozzám legközelebb jelenleg: Jaroslav Jezek (pillanatnyilag a feleségemmel nála lakunk Prágában), Ralph McKenzie (rendszeresen levelezünk matematikáról), és Petar Markovic (Újvidéken él, rendszeresen meglátogatom, de most éppen a Vanderbilt Egyetemen van). Minden esetben nagyon fontos a személyes kontaktus, évente legalább egyszer huzamosabb idıre (minimum 1-2 hét). Már az is hatalmas segítség, ha valaki meghallgat, megérti a kutatási témát és a nehézségeket. Ha igazán jó a téma, akkor ezek után közös kutatás kezdıdhet, ahol mindig az a kérdés, hogy másnap reggelre ki milyen eredménnyel tud elırukkolni. Sokszor a közös beszélgetés visz elıre, de számomra kell a magányos munka is.

-Volt évfolyamtársaiddal tartjátok-e a kapcsolatot? Hogyan? Ők mivel foglalkoznak? 

-Igen, főleg személyesen, és ebben szerencsém van, hogy évfolyamom 60%-a jelenleg a Bolyai Intézetben dolgozik. Sajnos a maradék két évfolyamtársammal ritkán találkozom.

-Szabadidődben mivel foglalkozol szívesen?

 -Nagyon szeretek kirándulni és hegyet mászni. A régi gimnazista osztálytársaimmal tartom leginkább a kapcsolatot, és nyaranta / telente velük megyünk közösen külföldre és otthoni utakra is. Ezen kívül nagyon érdekel, hogy mi történik az űrkutatásban, bár sajnos aktívan ebben nem vehetek részt. 

-Mit üzensz az SZTE TTIK volt és jelenlegi hallgatóinak (vagy akár a középiskolás diákoknak)?

-Azzal foglalkozzanak, amit szeretnek, és amiben lehetıleg a felső 90%-ba kerülhetnek. Ebben nincs ellentmondás, nagyon sok lehetőség van az életben, és mindenki lehet valamilyen témában a felső 90%-ban. A kérdés csak az, hogy abból meg is tud-e élni. A másik tanácsom az, hogy ha valakinek van lehetősége (és mostanában nagyon sok lehetőség van erre), akkor mindenképpen menjen el külföldre élni minimum egy fél évet, és utána jöjjön haza Magyarországra, hogy a kint szerzett tudást otthon is tudja kamatoztatni. Sokkal többen tudnák értékelni azt a sok jót Magyarországon, amit most észre sem vesznek, és jobban észrevennék azt, amin tényleg változtatni kellene.

-Köszönöm a beszélgetést! 

Horváth Eszter

Miklós Maróti weboldal URL

Horváth Eszter interjúja Maróti Miklóssal URL

Konzervatórium helyett választotta a számok világát URL

Vanderbilt team wins $1M in DARPA spectrum challenge finale URL

SMOG-P / ATL-1 telemetria URL

Martin Lajos (1827-1897)

Forrás a képre kattintva látható.

Martin Lajos 1827. augusztus 30-án Budán, jó körülmények között élő, birtokos családból. A szülők gondot fordítottak gyermekeik oktatására, a fiatal Martin Lajost kezdetben Horváth András házitanító oktatta, majd a budai evangélikus általános iskolában tanult. A gimnáziumot szintén Budán végezte, majd 1844-ben a pesti egyetem bölcsészkarán kezdte tanulmányait. 1847-ben mérnöki tanfolyamra ment. A szabadságharc alatt honvéd tüzér volt. A világosi fegyverletételkor Borosjenőnél megszökött a cári előőrsök elől, egy ideig bujdosott, majd rövid fogságot szenvedett, és közkatonaként besorozták az osztrák hadseregbe. Itt a tüzérségi röppentyűk tökéletesítése foglalkoztatta. A repülés problémájával 1856 körül kezdett behatóbban foglalkozni. Miután kilépett a hadsereg kötelékéből, 1860-ban mérnökként kezdett dolgozni. 1861-ben Buda városának főmérnöke lett; ugyanebben az évben a Magyar Tudományos Akadémia levelező taggá választotta. Tanított Selmecbányán majd 1869-től Pozsonyban. A tanítás mellett folytatta a korábban elkezdett ballisztikai kísérleteit és számításait. 1871-75 között megépítette a madárrepülést utánzó ornithopter repülőgépét. Belátva, hogy a repülés kérdése ilyen módon nem oldható meg, érdeklődése a propeller és a szélkerék felé fordult. Magyarországon ő volt az első, aki a repülőgép, illetve a kormányozható léghajó elméletével foglalkozott. Konstruált egy helikopterszerű, kerékpár-meghajtással működő szerkezetet, amely állítólag két-három méter magasra felemelkedett. A modell ma a kolozsvári történeti múzeumban található.

 “Eddig ágyú és tüzérség döntött a csatában, ezentúl a repülőgép veszi át a vezető szerepet. Egyszóval, a népek nemcsak szárazföldön és vízen, hanem levegőben is fognak egymásra rontani, s a hadjáratok sorsa és sikere nem annyira az ágyúk és bakák, mint inkább a repülőgépek számától, nagyságától s ügyes vezényletétől fog függeni” – mondta Martin Lajos, az 1800-as évek végén. Külföldről több ajánlatot kapott szabadalmának megvásárlására, de Martin nem volt hajlandó találmányát idegen országnak átengedni. Ezzel párhuzamosan a hidraulika is foglalkoztatta. Hajócsavar-mintapéldányát sikerrel alkalmazta a Lloyd angol hajótársaság. A gőzturbina alapelvének korai megfogalmazása is az ő érdeme. Foglalkozott a szélerőgépek kutatásával is.

Jókai Mór róla mintázta A jövő század regénye főhősét, Tatrangi Dávidot.

1872-ben kinevezték a kolozsvári egyetem matematika tanszékére, ahol haláláig működött. Az első tanévben a csillagászatot is ő oktatta. Négy alkalommal egy-egy tanéven át ő volt a matematika-természettudományi kar dékánja, majd 1895–96-ban az egyetem rektori tisztségét töltötte be. Rektori beköszönő beszédében a repülőgép jövőjét méltatta: “Új életviszonyok fognak fejlődni; a közlekedés függetlenebb lesz a vasúti rendszer hálózatától… a társadalom új nemzetközi szerződések s egyezmények által fogja magát biztosítani.”

Bár ez irányú elméleti megfontolásai a fizika szempontjából el nem fogadható egyszerűsítő feltevéseken alapultak, később mégis más magyar matematikusok (Réthy Mór, Kőnig Gyula, Vályi Gyula, Kürschák József) részére jelentős matematikai vizsgálatok kiindulópontjaivá váltak. 1897. márc. 4-én Kolozsváron hunyt el, síremléke a Házsongárdi temetőben található.

  • A középfuterő befolyása a forgatott test szilárdságára. 1861
  • Az erőműtani csavarfelületek. A vízszintes szélkerék elmélete. Budapest, 1875
  • A változtatási hánylat alkalmazása a propeller felület egyenleteinek lefejtésére. Budapest, 1877
  • A madárrepülés általános elmélete. Kolozsvár, 1891
  • A lebegő kerék bemutatója. Erdélyi Múzeum-Egyesület orvosi és természettudományi értesítője, 1893
  • A repülőgépről. Magyar Mérnök és Építész Egylet Közl. 1894
  • Gaal György: Egyetem a Farkas utcában: A kolozsvári Ferenc József Tudományegyetem előzményei, korszakai és vonzatai. Kolozsvár: Erdélyi Magyar Műszaki Tudományos Társaság. 2001. ISBN 973 0 02284 4 URL
  • Martin Lajos története URL
  • 190 éve született Martin Lajos matematikus, feltaláló URL
  • Darvay Tamás : Az első erdélyi repülőgép, a kolozsvári “lebegő kerék” URL
  • Heinrich László: Az első kolozsvári csillagda. Bukarest: Kriterion. 1978. 64–65. o.
  • Magyar életrajzi lexikon I–IV. Főszerk. Kenyeres Ágnes. Budapest: Akadémiai. 1967–1994.
  • Nemeskürty István: A kőszívű ember unokái. Budapest: Magvető. 1987. ISBN 963-14-1033-1
  • Szinnyei József: Magyar írók élete és munkái VIII. (Löbl–Minnich). Budapest: Hornyánszky. 1902. URL
  • Asztalos Lajos: Martin Lajos, a repülés kolozsvári úttörője, Szabadság, 2010. január 10. URL
  • Bitay Enikő, Máté Márton: Martin Lajos, a feltaláló mérnök és lebegőkereke, Fiatal Műszakiak Tudományos Ülésszaka XVIII., pp. 77–82. Erdélyi Múzeum-Egyesület, Kolozsvár 2013. ISSN 2067-6808.
  • Sebők István – Láris Ferenc: Martin Lajos hadmérnök-akadémikus munkássága URL
  • Martin Lajos Wikipédia URL
  • MIHOLCSA GYULA – MARTIN LAJOS dokumentumfilm URL

Megyesi László (1939-2015)

Forrás a képre kattintva látható.

Megyesi László 1939. május 11-én született Makón. Egyetemi tanulmányait a József Attila Tudományegyetemen 1958-ban matematika-fizika tanári szakon kezdte, majd matematikatanári-matematikus szakon folytatva 1963-ban szerzett diplomát. Végzése után azonnal a Bolyai Intézet Algebra és Számelmélet Tanszékére került, 1977-ben egyetemi docenssé nevezték ki, és itt dolgozott 2009-ig, nyugdíjba vonulásáig. Több mint tíz éven át, 1993 és 2004 között a tanszék vezetőjeként tevékenykedett. Alapítása óta tagja volt az SZTE Matematika- és Számítástudományok Doktori Iskolájának, társ-témavezetésével egy tanítványa szerzett doktori fokozatot.

Egyetemi doktori címét Rédei László témavezetésével 1969-ben szerezte, majd a korszak egyik vezető félcsoport-elméleti kutatója, E. S. Ljapin (Leningrád, ma Szentpétervár) aspiránsaként 1975-ben a matematikai tudományok kandidátusa lett. Pályája kezdetén Rédei László és Pollák György mellett részt vett a szegedi félcsoport-elméleti műhely munkájának elindításában. Kutatási eredményei is, melyeket részben Pollák Györggyel közösen ért el, elsősorban a félcsoportok szerkezetének jobb megértését segítették elő. Később Huhn Andrással számelméleti, Csákány Bélával univerzális algebrai témában is végzett közös kutatásokat.

Lelkiismeretes és népszerű oktató volt, speciálkollégiumait sok hallgató látogatta, és számos hallgató szakdolgozatának és diplomamunkájának volt témavezetője. Különösen a tanárképzést tartotta szívügyének. Az elmúlt évtizedek alatt az Algebra és Számelmélet Tanszék által oktatott kötelező tárgyak jelentős részét tanította. Oktatási tapasztalatait egyetemi jegyzetekben és tankönyvekben foglalta össze.

1964-től 1989-ig a MTESZ Csongrád Megyei Választmányának tagja, 1966-tól ugyaneddig a Bolyai János Matematikai Társulat Csongrád Megyei Tagozatának titkára volt. Az Algebra és Számelmélet Tanszék által az 1970-es évek elején elindított nemzetközi algebrai konferenciasorozat szervezési munkájában több mint két évtizeden keresztül tevékenyen részt vett. Harminc év óta társszerkesztője volt a Bolyai Intézet nemzetközi matematikai folyóiratának, az Acta Scientiarum Mathematicarumnak. 1999 és 2006 között rendszeresen tartott előadást a Bolyai Intézet oktatói által a Romániai Magyar Pedagógus Szövetség tagjai számára szervezett évközi tanártovábbképzéseken, és két alkalommal a Szövetség Bolyai Nyári Akadémiájának is meghívott előadója volt.

Oktató-kutató munkája, valamint közéleti tevékenysége elismeréseképpen 1980-ban Kiváló Munkáért kitüntetésben részesült, 1984-ben pedig MTESZ Díjat kapott.

Amilyen szerényen élt, olyan csendben ment el kollégánk, akitől az oktatás szeretetét tanultuk, akire mindig számíthattunk, és akitől még a parázs viták hevében sem hallottunk egyetlen hangos szót sem. Emléke itt marad velünk.

Szegedi Tudományegyetem Bolyai Intézete

Megyesi Lászlót 2015. október 16-án, pénteken délelőtt 11 órakor kísérjük utolsó útjára a szegedi Alsóvárosi temetőben.

 

További olvasásra URL

Következő oldal

© 2021 Szegedi Tudományegyetem Klebelsberg Kuno Könyvtára -  Minden jog fenntartva.